Awesome
Update 11/06/17: FISTA with backtracking is tested with lasso, lasso_weighted, and Elastic net.
A simple implementation of FISTA
A MATLAB FISTA implementation based on the paper:
A. Beck and M. Teboulle, "A fast iterative shrinkage-thresholding algorithm for linear inverse problems", SIAM Journal on Imaging Sciences, vol. 2, no. 1, pp. 183–202, 2009. View the paper.
Tiep Vu, Penn State, Sep 2016
If you find any issue, please let me know via this. I would really appreciate. Thank you.
Note: Results in this repo are compared with those obtained by the SPAMS toolbox. You need to install spams and put the generated 'build' folder under the 'spams' folder of this repo.
Table of content
<!-- MarkdownTOC --> <!-- /MarkdownTOC --><a name="general-optimization-problem"></a>
General Optimization problem
<img src = "latex/fista1.png" height = "30"/>where:
g: R^n -> R: a continuous convex function which is possibly nonsmooth.
f: R^n -> R: a smooth convex function of the typeC^{1, 1}, i.e., continuously differentiable with Lipschitz continuous gradientL(f):||grad_f(x) - grad_f(y)|| <= L(f)||x - y||for everyx, y \in R^n
Note: this implementation also work on nonnegativity constrained problems.
<a name="algorithms"></a>
Algorithms
<a name="if-lf-is-easy-to-calculate"></a>
If L(f) is easy to calculate,
We use the following algorithm:
 where
where pL(y) is a proximal function defined as:
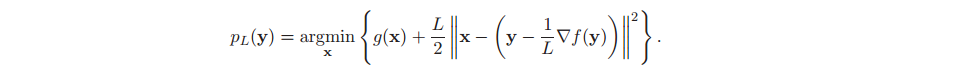
For a new problem, our job is to implement two functions: grad_f(x) and pL(y) which are often simpler than the original optimization stated in (1).
<a name="in-case-lf-is-hard-to-find"></a>
In case L(f) is hard to find,
We can alternatively use the following algorithm:
 where
where QL(x, y) is defined as:
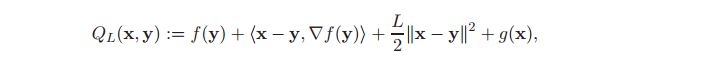
<a name="usage"></a>
Usage
<a name="fistageneralm"></a>
fista_general.m
[X, iter, min_cost] = fista_general(grad, proj, Xinit, L, opts, calc_F)
See fista_general.m.
where:
INPUT:
grad : a function calculating gradient of f(X) given X.
proj : a function calculating pL(x) -- projection
Xinit : a matrix -- initial guess.
L : a scalar the Lipschitz constant of the gradient of f(X).
opts : a struct
opts.lambda : a regularization parameter, can be either a scalar or
a weighted matrix.
opts.max_iter: maximum iterations of the algorithm.
Default 300.
opts.tol : a tolerance, the algorithm will stop if difference
between two successive X is smaller than this value.
Default 1e-8.
opts.verbose : showing F(X) after each iteration or not.
Default false.
calc_F: optional, a function calculating value of F at X
via feval(calc_F, X).
OUTPUT:
X : solution
iter : number of run iterations
min_cost : the achieved cost
<a name="fistabacktracking"></a>
fista_backtracking
function X = fista_backtracking(calc_f, grad, Xinit, opts, calc_F)
See fista_backtracking.m
where:
INPUT:
calc_f : a function calculating f(x) in F(x) = f(x) + g(x)
grad : a function calculating gradient of f(X) given X.
Xinit : a matrix -- initial guess.
opts : a struct
opts.lambda : a regularization parameter, can be either a scalar or
a weighted matrix.
opts.max_iter: maximum iterations of the algorithm.
Default 300.
opts.tol : a tolerance, the algorithm will stop if difference
between two successive X is smaller than this value.
Default 1e-8.
opts.verbose : showing F(X) after each iteration or not.
Default false.
opts.L0 : a positive scalar.
opts.eta: (must be > 1). eta in the algorithm (page 194)
calc_F: optional, a function calculating value of F at X
via feval(calc_F, X).
OUTPUT:
X : solution
<a name="examples"></a>
Examples
<a name="lasso-and-weighted-problems"></a>
Lasso (and weighted) problems
Optimization problem: This function solves the l1 Lasso problem:
<img src = "latex/fista_lasso1.png" height = "40"/>if lambda is a scalar, or :
if lambda is a matrix. In case lambda is a vector, it will be converted to a matrix with same columns and its # of columns = # of columns of X.
MATLAB function:
function X = lasso_fista(Y, D, Xinit, opts)
opts = initOpts(opts);
lambda = opts.lambda;
if numel(Xinit) == 0
Xinit = zeros(size(D,2), size(Y,2));
end
%% cost f
function cost = calc_f(X)
cost = 1/2 *normF2(Y - D*X);
end
%% cost function
function cost = calc_F(X)
if numel(lambda) == 1 % scalar
cost = calc_f(X) + lambda*norm1(X);
elseif numel(lambda) == numel(X)
cost = calc_f(X) + norm1(lambda.*X);
end
end
%% gradient
DtD = D'*D;
DtY = D'*Y;
function res = grad(X)
res = DtD*X - DtY;
end
%% Checking gradient
if nargin == 0 && opts.check_grad
check_grad(@calc_f, @grad, Xinit);
end
%% Lipschitz constant
L = max(eig(DtD));
%% Use fista
[X, ~, ~] = fista_general(@grad, @proj_l1, Xinit, L, opts, @calc_F);
end
(See [])
Example:
1. L1 minimization (lambda is a scalar)
See demo_lasso.m
function test_lasso()
clc
d = 300; % data dimension
N = 70; % number of samples
k = 100; % dictionary size
lambda = 0.01;
Y = normc(rand(d, N));
D = normc(rand(d, k));
%% cost function
function c = calc_F(X)
c = 0.5*normF2(Y - D*X) + lambda*norm1(X);
end
%% fista solution
opts.pos = true; % change to false for unconstrained problems
opts.lambda = lambda;
X_fista = lasso_fista(Y, D, [], opts);
%% spams solution
param.lambda = lambda;
param.lambda2 = 0;
param.numThreads = 1;
param.mode = 2;
param.pos = opts.pos;
X_spams = mexLasso(Y, D, param);
%% compare costs
cost_spams = calc_F(X_spams);
cost_fista = calc_F(X_fista);
fprintf('cost_fista = %.5s\n', cost_fista);
fprintf('cost_spams = %.5s\n', cost_spams);
end
will generate an output like this:
cost_fista = 8.39552e+00
cost_spams = 8.39552e+00
2. Weighted l1 minimization (lambda is a vector or a matrix)
3. Full test
Run fista_lasso_fulltest.m to see the full test.
Results should look like this:
A toy example:
Data dimension : 300
No. of samples : 70
No. of atoms in the dictionary: 100
=====================================================
Lasso FISTA solution vs SPAMS solution,
both of the following values should be close to 0.
1. average(norm1(X_fista - X_spams)) = 0.000028
2. costfista - cost_spams = 0.000003
SPAMS provides a better cost.
=====================================================
Lasso Weighted FISTA solution vs SPAMS solution,
both of the following values should be close to 0.
1. average(norm1(X_fista - X_spams)) = 0.000015
2. costfista - cost_spams = -0.000004
FISTA provides a better cost.
================Positive Constraint===================
Lasso FISTA solution vs SPAMS solution,
both of the following values should be close to 0.
1. average(norm1(X_fista - X_spams)) = 0.000025
2. costfista - cost_spams = 0.003537
SPAMS provides a better cost.
================Positive Constraint===================
Lasso Weighted FISTA solution vs SPAMS solution,
both of the following values should be close to 0.
1. average(norm1(X_fista - X_spams)) = 0.000016
2. costfista - cost_spams = -0.000005
FISTA provides a better cost.
<a name="elastic-net-problems"></a>
Elastic net problems
Optimization problem: This function solves the Elastic Net problem:
<img src = "latex/fista_elastic.png" height = "40"/>if lambda is a scalar, or :
if lambda is a matrix. In case lambda is a vector, it will be convert to a matrix with same columns and its # of columns = # of columns of X.
MATLAB function:
See fista_enet.m
function X = fista_enet(Y, D, Xinit, opts)
opts = initOpts(opts);
lambda = opts.lambda;
lambda2 = opts.lambda2;
if numel(lambda) > 1 && size(lambda, 2) == 1
lambda = repmat(opts.lambda, 1, size(Y, 2));
end
if numel(Xinit) == 0
Xinit = zeros(size(D,2), size(Y,2));
end
%% cost f
function cost = calc_f(X)
cost = 1/2 *normF2(Y - D*X) + lambda2/2*normF2(X);
end
%% cost function
function cost = calc_F(X)
if numel(lambda) == 1 % scalar
cost = calc_f(X) + lambda*norm1(X);
elseif numel(lambda) == numel(X)
cost = calc_f(X) + norm1(lambda.*X);
end
end
%% gradient
DtD = D'*D + lambda2*eye(size(D, 2));
DtY = D'*Y;
function res = grad(X)
res = DtD*X - DtY;
end
%% Checking gradient
if opts.check_grad
check_grad(@calc_f, @grad, Xinit);
end
%% Lipschitz constant
L = max(eig(DtD));
%% Use fista
opts.max_iter = 500;
[X, ~, ~] = fista_general(@grad, @proj_l1, Xinit, L, opts, @calc_F);
end
Example:
See demo_enet.m
<a name="row-sparsity-problems"></a>
Row sparsity problems
Optimization problem:
<img src = "latex/fista_row_sparsity0.png" height = "50"/>where 'm' is number of rows and <img src = "latex/fista_row_sparsity1.png" height = "15"/> is the i-th row of <img src = "latex/fista_row_sparsity2.png" height = "15"/>.
Matlab function:
function X = fista_row_sparsity(Y, D, Xinit, opts)
opts = initOpts(opts);
lambda = opts.lambda;
if numel(lambda) > 1 && size(lambda, 2) == 1
lambda = repmat(opts.lambda, 1, size(Y, 2));
end
if numel(Xinit) == 0
Xinit = zeros(size(D,2), size(Y,2));
end
%% cost f
function cost = calc_f(X)
cost = 1/2 *normF2(Y - D*X);
end
%% cost function
function cost = calc_F(X)
cost = calc_f(X) + lambda*norm12(X);
end
%% gradient
DtD = D'*D;
DtY = D'*Y;
function res = grad(X)
res = DtD*X - DtY;
end
%% Checking gradient
if opts.check_grad
check_grad(@calc_f, @grad, Xinit);
end
%% Lipschitz constant
L = max(eig(DtD));
%% Use fista
opts.max_iter = 500;
[X, ~, ~] = fista_general(@grad, @proj_l12, Xinit, L, opts, @calc_F);
Example:
function test_row_sparsity()
clc
d = 30; % data dimension
N = 70; % number of samples
k = 50; % dictionary size
lambda = 0.01;
Y = normc(rand(d, N));
D = normc(rand(d, k));
%% cost function
function c = calc_F(X)
c = 0.5*normF2(Y - D*X) + lambda*norm12(X);
end
%% fista solution
opts.pos = true;
opts.lambda = lambda;
opts.check_grad = 0;
X_fista = fista_row_sparsity(Y, D, [], opts);
cost_fista = calc_F(X_fista);
fprintf('cost_fista = %.5s\n', cost_fista);
end
<a name="group-sparsity-problems-implement-later"></a>