Home

Awesome

PyPI 📦 PyTests Downloads

Log Periodic Power Law Singularity (LPPLS) Model

lppls is a Python module for fitting the LPPLS model to data.

Overview

The LPPLS model provides a flexible framework to detect bubbles and predict regime changes of a financial asset. A bubble is defined as a faster-than-exponential increase in asset price, that reflects positive feedback loop of higher return anticipations competing with negative feedback spirals of crash expectations. It models a bubble price as a power law with a finite-time singularity decorated by oscillations with a frequency increasing with time.

Try the demo:

Open In Colab

Here is the model:

E[ln\ p(t)] = A + B(t_c-t)^{m}+C(t_c-t)^{m}\cos(\omega\ ln(t_c-t) - \phi)

where:

The model has three components representing a bubble. The first, $A+B(t_c-t)^{m}$, handles the hyperbolic power law. For $m$ < 1 when the price growth becomes unsustainable, and at $t_c$ the growth rate becomes infinite. The second term, $C(t_c-t)^{m}$, controls the amplitude of the oscillations. It drops to zero at the critical time $t_c$. The third term, $\cos(\omega\ ln(t_c-t) - \phi)$, models the frequency of the oscillations. They become infinite at $t_c$.

Important links

Installation

Dependencies

lppls requires:

User installation

pip install -U lppls

Example Use

from lppls import lppls, data_loader
import numpy as np
import pandas as pd
from datetime import datetime as dt
%matplotlib inline

# read example dataset into df 
data = data_loader.nasdaq_dotcom()

# convert time to ordinal
time = [pd.Timestamp.toordinal(dt.strptime(t1, '%Y-%m-%d')) for t1 in data['Date']]

# create list of observation data
price = np.log(data['Adj Close'].values)

# create observations array (expected format for LPPLS observations)
observations = np.array([time, price])

# set the max number for searches to perform before giving-up
# the literature suggests 25
MAX_SEARCHES = 25

# instantiate a new LPPLS model with the Nasdaq Dot-com bubble dataset
lppls_model = lppls.LPPLS(observations=observations)

# fit the model to the data and get back the params
tc, m, w, a, b, c, c1, c2, O, D = lppls_model.fit(MAX_SEARCHES)

# visualize the fit
lppls_model.plot_fit()

# should give a plot like the following...

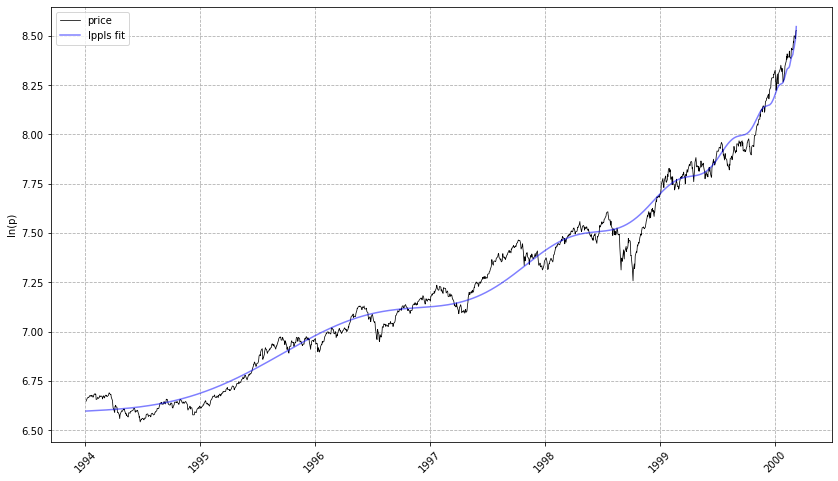
LPPLS Fit to the Nasdaq Dataset

# compute the confidence indicator
res = lppls_model.mp_compute_nested_fits(
    workers=8,
    window_size=120, 
    smallest_window_size=30, 
    outer_increment=1, 
    inner_increment=5, 
    max_searches=25,
    # filter_conditions_config={} # not implemented in 0.6.x
)

lppls_model.plot_confidence_indicators(res)
# should give a plot like the following...

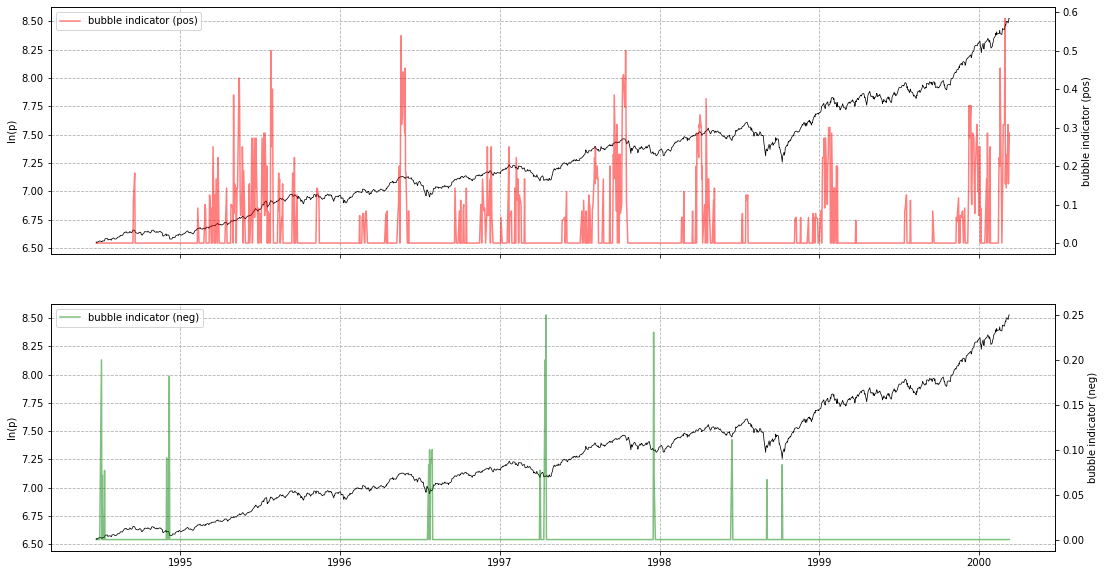
LPPLS Confidnce Indicator

If you wish to store res as a pd.DataFrame, use compute_indicators.

<details> <summary>Example</summary> 
res_df = lppls_model.compute_indicators(res)
res_df
# gives the following...
<img src="https://raw.githubusercontent.com/Boulder-Investment-Technologies/lppls/master/img/compute_indicator_df.png" width="500"/> </details>

Quantile Regression

Based on the work in Zhang, Zhang & Sornette 2016, quantile regression for LPPLS uses the L1 norm (sum of absolute differences) instead of the L2 norm and applies the q-dependent loss function during calibration. Please refer to the example usage here.

Other Search Algorithms

Shu and Zhu (2019) proposed CMA-ES for identifying the best estimation of the three non-linear parameters ($t_c$, $m$, $\omega$).

The CMA-ES rates among the most successful evolutionary algorithms for real-valued single-objective optimization and is typically applied to difficult nonlinear non-convex black-box optimization problems in continuous domain and search space dimensions between three and a hundred. Parallel computing is adopted to expedite the fitting process drastically.

This approach has been implemented in a subclass and can be used as follows... Thanks to @paulogonc for the code.

from lppls import lppls_cmaes
lppls_model = lppls_cmaes.LPPLSCMAES(observations=observations)
tc, m, w, a, b, c, c1, c2, O, D = lppls_model.fit(max_iteration=2500, pop_size=4)

Performance Note: this works well for single fits but can take a long time for computing the confidence indicators. More work needs to be done to speed it up.

References