Awesome

Contact

For cooperation you can contact serge dot rogatch at gmail dot com.

Interoperability

.NET: https://github.com/srogatch/ProbQA/tree/master/ProbQA/ProbQANetCore

Python: https://github.com/srogatch/ProbQA/tree/master/Interop/Python/ProbQAInterop

You can also view the examples of usage from Python in the source code of the website: https://github.com/srogatch/probqa-web

Applications

An application of the probabilistic question-asking system is now available as a website (source code: https://github.com/srogatch/probqa-web ) : http://probqa.com/ or http://best-games.info , an interactive recommendation engine for games. Here users can find the next game to play without knowing its name or keywords. The users only need to answer questions, and the program lists the top recommendations for each user. The engine that powers the website is supposed to work similarly to a popular game Akinator, where the user thinks of a character, and the program asks questions to guess about the user's secret character.

In ProbQA there is no secret: the user simply doesn't know exactly what he/she wants. So the program asks questions to come up with something suitable for the user.

After trying the interactive recommendation engine, you can take a survey https://www.surveymonkey.com/r/SMJ2ZRZ

ProbQA

In terms of Applied AI goals, it's an expert system. Specifically, it's a probabilistic question-answering system: the program asks, the users answer. The minimal goal of the program is to identify what the user needs (a target), even if the user is not aware of the existence of such a thing/product/service. It is just a backend in C++. It's up to the others to implement front-ends for their needs. The backend can be applied to something like this http://en.akinator.com/ , or for selling products&services in some internet-shops (as a chat-bot helping users to determine what they need, even if they can't formulate the keywords or even their desires specifically).

Below are the learning curves of the program for matrix size 5 000 000: it's 1000 questions times 5 answer options for each question, times 1000 targets. In this experiment we train the program for binary search: the range of targets Tj is 0 to 999, and each question Qi is "How does your guess compare to Qi?". The answer options are 0 - "The guess is much lower than Qi", 1 - "The guess is a bit lower than Qi", 2 - "The guess exactly equals Qi", 3 - "The guess is a bit higher than Qi" and 4 - "The guess is much higher than Qi".

X-axis contains the number of questions asked&answered (up to 5 million). Y-axis contains for each 256 quizzes in a row the percentage of times the program correctly listed the guessed target among top 10 most probable targets. Note that testing is always on novel data: we first choose a random number, then let the program guess it by asking questions and getting answers from us, then either after the program has guessed correctly or asked more than 100 questions (meaning a failure), we teach the program, revealing it our selected random number.

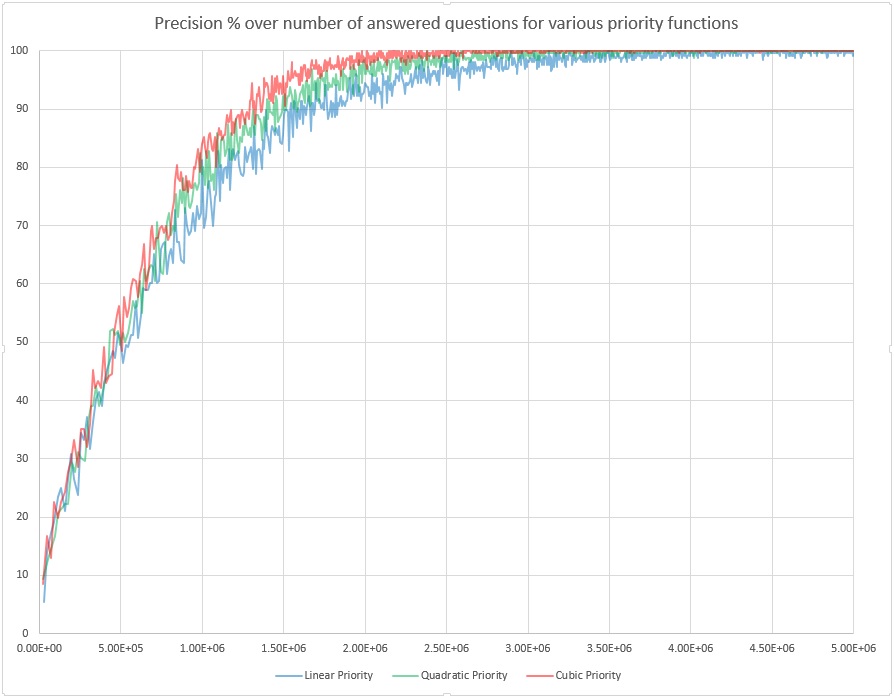
From the data&diagram it seems that the program learns faster and reaches higher precision for priority functions which give more preference to lower-entropy options. So perhaps some exponential priority function can give superior results. But so far I don't know how to implement it without overflow. The priority function is in file ProbQA\ProbQA\PqaCore\CEEvalQsSubtaskConsider.cpp , near the end of it currently .

There is also a flaw currently in the key theory, which makes the program stubborn (I think it's close to "overfitting" term of Machine Learning). After the program mistakenly selects some target as the most probable, it start asking such questions which let it stick to its mistake, rather than questions which would let the program see that other targets are more probable. Although it is what happens in life, technically it is an error in the key algorithm/theory behind the program.

Update 2017-10-17: Faster learning and higher accuracy

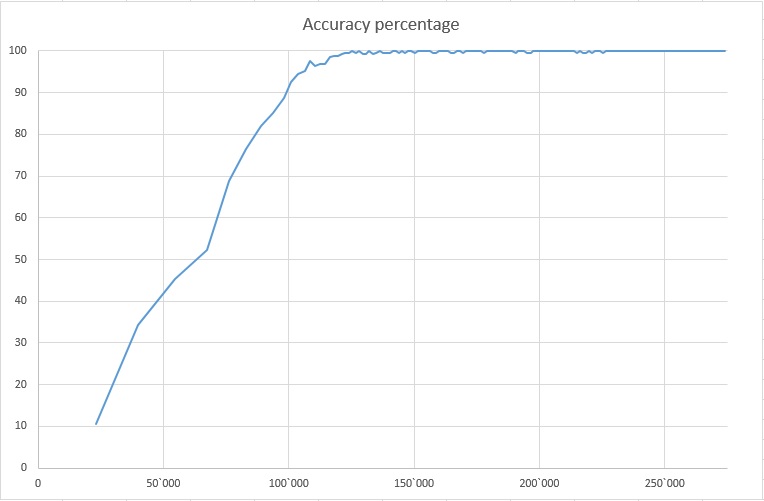
In the previous section I described a problem of the program bein stubborn: after convincing itself as if some wrong target is the most probable, the program was starting to ask questions which let it stick to its mistake, rather than learning the truth. I think I have solved this problem by changing the priority function from entropy-only based to distance&entropy based. Rather than just minimizing the entropy of posterior probabilities, it now also takes into account the Euclidean distance between prior and posterior probability vectors. This has allowed the program to learn 20 times faster. It now starts listing in top 10 the guessed target in almost 100% cases after about 125 000 of questions asked&answered (for a matrix of 1000 questions times 5 answers times 1000 targets). See the Accuracy graph.

After the abovementioned initial training, it reaches positive result on average in 4.3 questions asked (by the program) and answered (by the user). See the graph below.

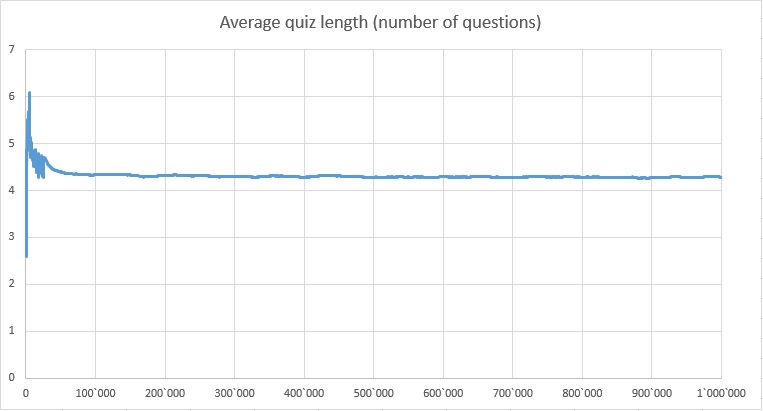
So that is quite competitive with the binary search algorithm programmed by a human. To narrow the search range from 1000 down to 10 targets, a human-programmed binary search algorithm would require 3.32 steps on average (it's base 4 logarithm of 100, because we have 5 answer options, of which one is just the strict equality).

However, human-programmed binary search algorithm doesn't tolerate mistakes and doesn't rate the targets by their probability of being the desired one. And of course it doesn't learn along the way. While probabilistic question-asking/answering system does this.

Moreover, I think there is some room for improvement in the priority function. Currently I use polynomial priority: pow(distance, 12) / pow(nExpectedTargets, 6), which empirically showed the best results in my limited number of priority function experimented with. Still I think that even better results can be produced with exponential priority function. Now let's see if it's better to devise and try some exponential functions now, or proceed with (less exciting) engineering tasks like saving&loading the knowledge base to&from a file, etc.

Update 2017-11-26: Ready to try (release 0.1.0.0)

Recently the implementation of loading and saving of the knowledge base was finished. Training and prediction were finished more than a month ago, and were tested/fixed and tuned after that.

What's not yet finished is resizing the KB. It will not be possible to change the number of answer options after a KB is created. However, I am still to implement the changing of the number of questions and targets.

You can try integrating the engine into your systems.

To compile you need MSVS2017 v15.4.2 or higher. An external dependency is gtest: https://github.com/google/googletest (only if you want to run tests or dislike compilation errors in unrelated projects too much).

Earlier I published the results of experiments for top 10 targets (where a target is considered to have been guessed correctly if it's listed among 10 most probable targets). Here's the result for more challenging task - guessing the targets among top 1, i.e. it must be selected as the single most probable target. After many experiments and tuning, currently the learning curve of accuracy looks like the following for learning binary search algorithm:

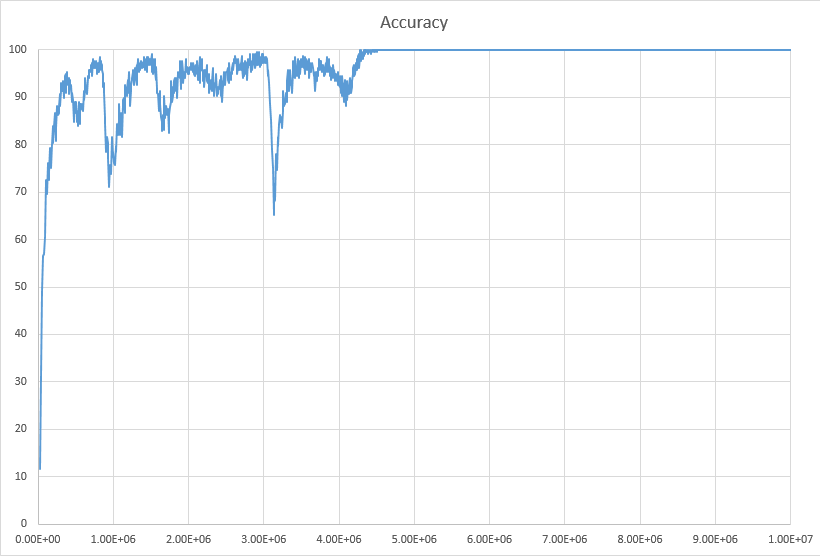
So for KB of size 1000 questions by 5 answer options by 1000 targets, the accuracy reaches 100% after about 4.5 millions of questions answered, and then stays at 100% too.

References

I'm analyzing memory leaks with Deleaker: https://www.deleaker.com/