Awesome

Planet-LOD - Spherical Level-of-Detail

License : MIT

http://opensource.org/licenses/MIT

Summary

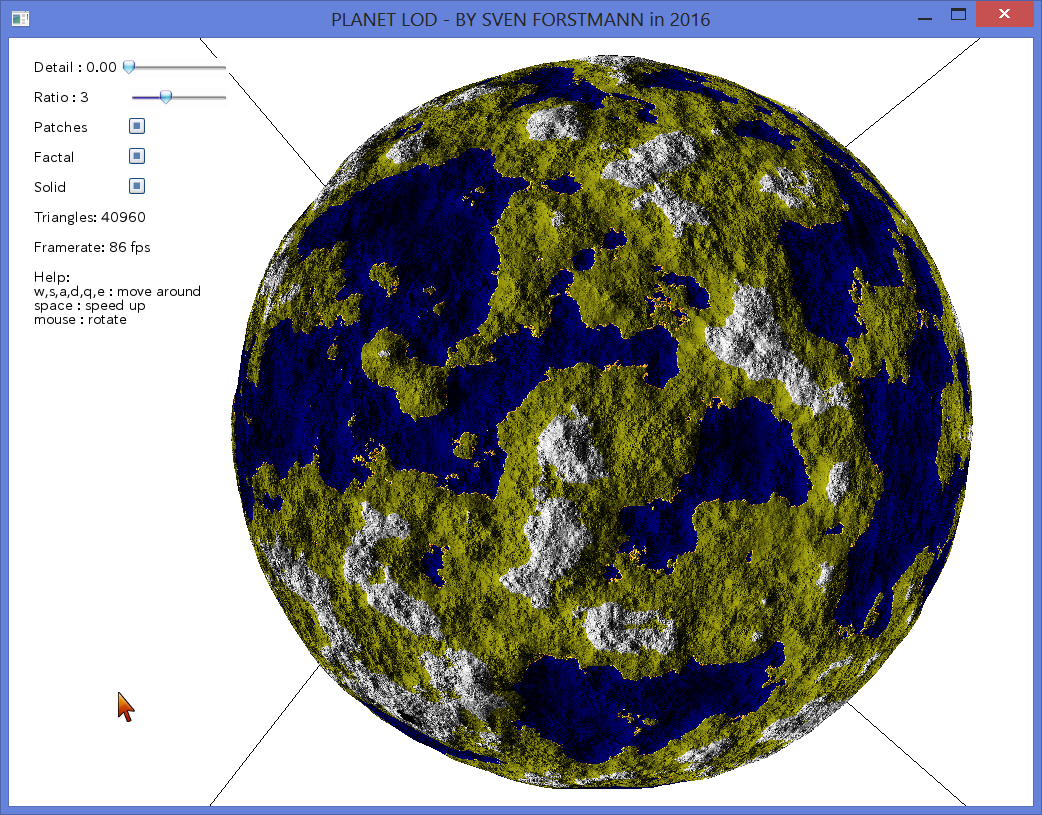
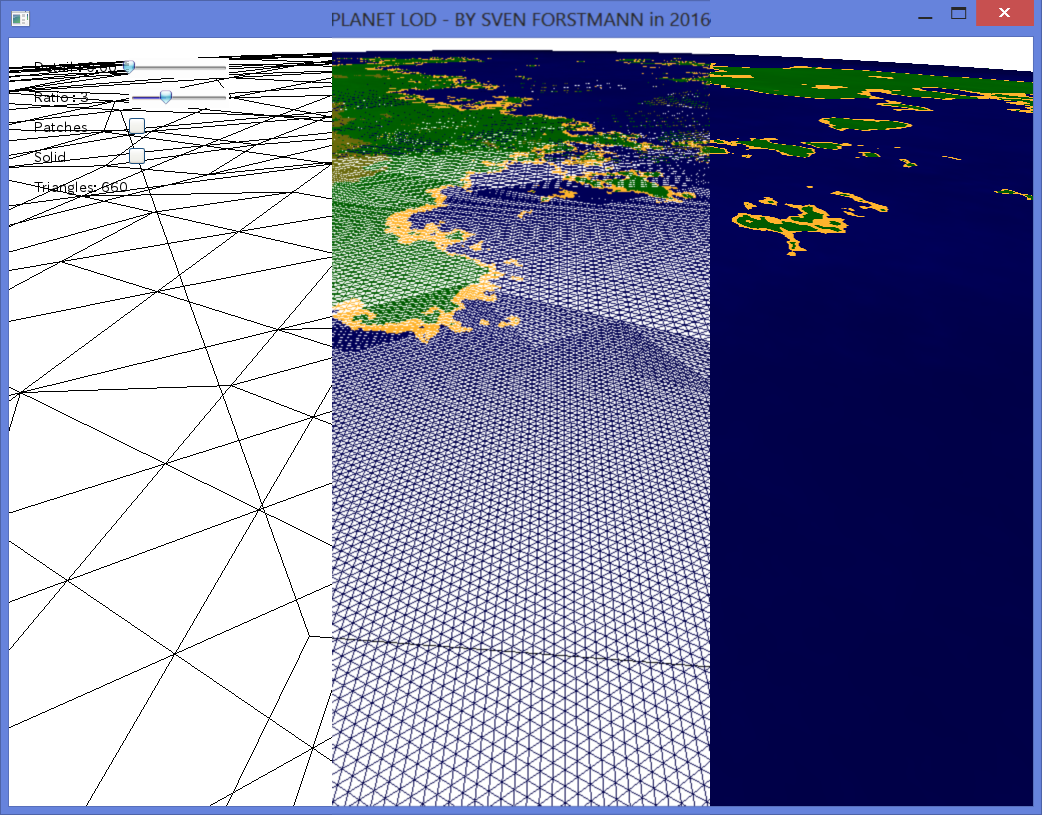
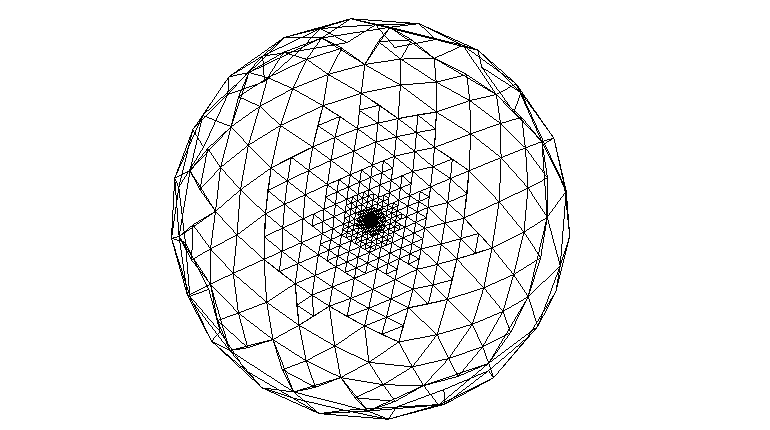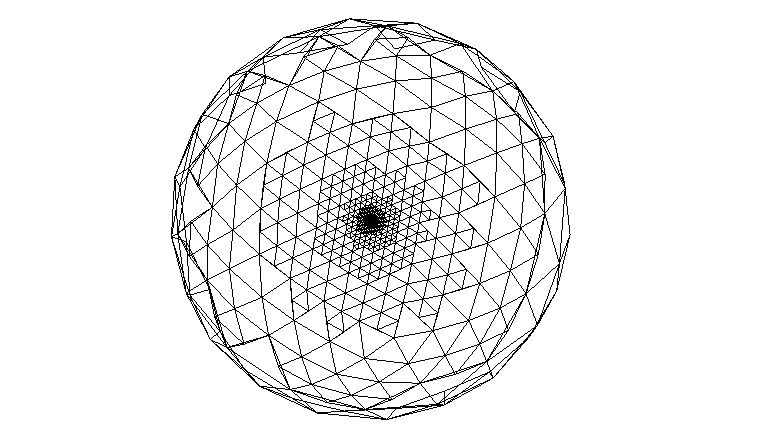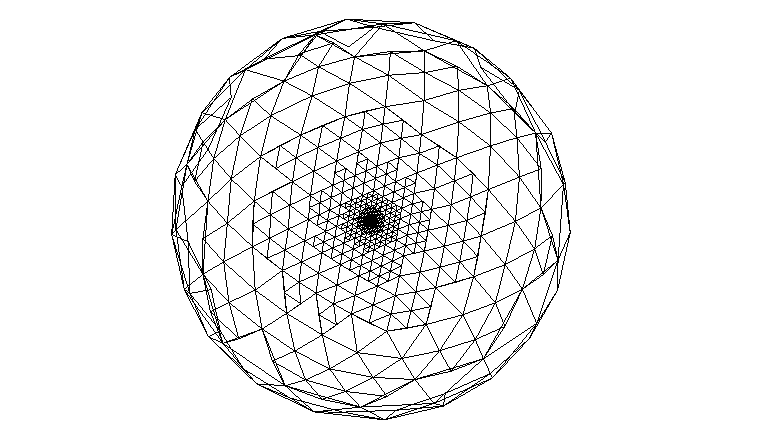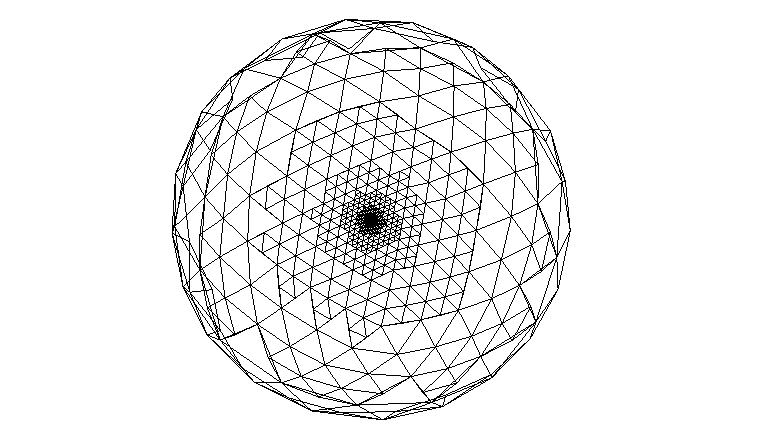
This is a simple tutorial of how to render planet using a triangle subdivision approach. The source is optimized for compactness and to make the algorithm easy to understand. The algorithm renders an icosahedron with 12 triangles, each of which is being sub-divided using a recursive function.

If you would render the planet in a game engine, you would have to render a triangle patch for NxN triangles with a VBO inside the draw_triangle function, rather than a single triangle with gl immediate mode. The center of detail is where the camera would be in the game. The camera in the demo is above for demonstration purpose.

What the code is :

• A simple demo to show how a planet rendering with LOD works
• As short as possible so you can experiment with the algorithm
• Easy to understand

What the code is not:

• A ready to use planet rendering library with shaders frustum culling etc
• A way to render a planet with best performance
• A demonstration of modern high performance gl rendering

Discussion Forum

http://www.gamedev.net/topic/677700-planet-rendering-spherical-level-of-detail-in-less-than-100-lines-of-c/ https://www.reddit.com/r/gamedev/comments/4d2oez/planet_rendering_spherical_levelofdetail_in_less/

Screenshot

struct World
{
	static void draw_triangle(vec3f p1, vec3f p2, vec3f p3)
	{
		glPolygonMode(GL_FRONT_AND_BACK, GL_LINE);
		glBegin(GL_TRIANGLES);
		glVertex3f(p1.x, p1.y, p1.z);
		glVertex3f(p2.x, p2.y, p2.z);
		glVertex3f(p3.x, p3.y, p3.z);
		glEnd();
		glPolygonMode(GL_FRONT_AND_BACK, GL_FILL);
	}
	static void draw_recursive(vec3f p1,vec3f p2,vec3f p3, vec3f center , float size=1)
	{
		float ratio = gui.screen[0].slider["lod.ratio"].val; // default : 1
		float minsize = gui.screen[0].slider["detail"].val;  // default : 0.01

		double dot = double(((p1+p2+p3)/3).dot(center));
		double dist = acos(clamp(dot, -1, 1)) / M_PI;

		if (dist > 0.5) return;//culling

		if (dist > double(ratio)*double(size) || size < minsize) 
		{ 
			draw_triangle(p1, p2, p3); 
			return; 
		}

		// Recurse
		
		vec3f p[6] = { p1, p2, p3, (p1 + p2) / 2, (p2 + p3) / 2, (p3 + p1) / 2 };
		int idx[12] = { 0, 3, 5, 5, 3, 4, 3, 1, 4, 5, 4, 2 };

		loopi(0, 4)
		{
			draw_recursive(
				p[idx[3 * i + 0]].norm(), 
				p[idx[3 * i + 1]].norm(),
				p[idx[3 * i + 2]].norm(),
				center,size/2 );
		}
	}
	static void draw(vec3f center)
	{
		// create icosahedron
		float t = (1.0 + sqrt(5.0)) / 2.0;

		std::vector<vec3f> p({ 
			{ -1, t, 0 }, { 1, t, 0 }, { -1, -t, 0 }, { 1, -t, 0 },
			{ 0, -1, t }, { 0, 1, t }, { 0, -1, -t }, { 0, 1, -t },
			{ t, 0, -1 }, { t, 0, 1 }, { -t, 0, -1 }, { -t, 0, 1 },
		});
		std::vector<int> idx({ 
			0, 11, 5, 0, 5, 1, 0, 1, 7, 0, 7, 10, 0, 10, 11,
			1, 5, 9, 5, 11, 4, 11, 10, 2, 10, 7, 6, 10, 7, 6, 7, 1, 8,
			3, 9, 4, 3, 4, 2, 3, 2, 6, 3, 6, 8, 3, 8, 9,
			4, 9, 5, 2, 4, 11, 6, 2, 10, 8, 6, 7, 9, 8, 1
		});

		loopi(0, idx.size() / 3)
		{
			draw_recursive(
				p[idx[i * 3 + 0]].norm(), // triangle point 1
				p[idx[i * 3 + 1]].norm(), // triangle point 2
				p[idx[i * 3 + 2]].norm(), // triangle point 3
				center);
		}
	}
};