Awesome

legged_control

NOTICE: This software is not supported anymore! The authors of this software are developing a completely new framework and are not working on this project anymore. Please excuse any inconvenience this might cause.

Publications

If you use this work in an academic context, please consider citing the following publications:

@misc{2407.21781,
Author = {Qiayuan Liao and Bike Zhang and Xuanyu Huang and Xiaoyu Huang and Zhongyu Li and Koushil Sreenath},
Title = {Berkeley Humanoid: A Research Platform for Learning-based Control},
Year = {2024},
Eprint = {arXiv:2407.21781},
}

Introduction

legged_control is an NMPC-WBC legged robot control stack and framework based on OCS2 and ros-control.

The advantage shows below:

To the author's best knowledge, this framework is probably the best-performing open-source legged robot MPC control framework;
You can deploy this framework in your A1 robot within a few hours;
Thanks to the ros-control interface, you can easily use this framework for your custom robot.

I believe this framework can provide a high-performance and easy-to-use model-based baseline for the legged robot community.

https://user-images.githubusercontent.com/21256355/192135828-8fa7d9bb-9b4d-41f9-907a-68d34e6809d8.mp4

Installation

Source code

The source code is hosted on GitHub: qiayuanliao/legged_control.

# Clone legged_control
git clone git@github.com:qiayuanliao/legged_control.git

OCS2

OCS2 is a huge monorepo; DO NOT try to compile the whole repo. You only need to compile ocs2_legged_robot_ros and its dependencies following the step below.

You are supposed to clone the OCS2, pinocchio, and hpp-fcl as described in the documentation of OCS2.

# Clone OCS2
git clone git@github.com:leggedrobotics/ocs2.git
# Clone pinocchio
git clone --recurse-submodules https://github.com/leggedrobotics/pinocchio.git
# Clone hpp-fcl
git clone --recurse-submodules https://github.com/leggedrobotics/hpp-fcl.git
# Clone ocs2_robotic_assets
git clone https://github.com/leggedrobotics/ocs2_robotic_assets.git
# Install dependencies
sudo apt install liburdfdom-dev liboctomap-dev libassimp-dev

Compile the ocs2_legged_robot_ros package with catkin tools instead of catkin_make. It will take you about ten minutes.
```
catkin config -DCMAKE_BUILD_TYPE=RelWithDebInfo
catkin build ocs2_legged_robot_ros ocs2_self_collision_visualization
```
Ensure you can command the ANYmal as shown in the document and below.

Build

Build the source code of legged_control by:

catkin build legged_controllers legged_unitree_description

Build the simulation (DO NOT run on the onboard computer)

catkin build legged_gazebo

Build the hardware interface real robot. If you use your computer only for simulation, you DO NOT need to compile legged_unitree_hw (TODO: add a legged prefix to the package name)

catkin build legged_unitree_hw

Quick Start

Set your robot type as an environment variable: ROBOT_TYPE

export ROBOT_TYPE=a1

Run the simulation:

roslaunch legged_unitree_description empty_world.launch

Or on the robot hardware:

roslaunch legged_unitree_hw legged_unitree_hw.launch

Load the controller:

roslaunch legged_controllers load_controller.launch cheater:=false

Start the legged_controller or legged_cheater_controller, NOTE that you are not allowed to start the legged_cheater_controller in real hardware!

rosservice call /controller_manager/switch_controller "start_controllers: ['controllers/legged_controller']                   
stop_controllers: ['']
strictness: 0
start_asap: false
timeout: 0.0"

Or, you can start the controller using rqt_controller_manager GUI:

sudo apt install ros-noetic-rqt-controller-manager
rosrun rqt_controller_manager rqt_controller_manager

Set the gait in the terminal of load_controller.launch, then use RViz (you need to add what you want to display by yourself) and control the robot by cmd_vel and move_base_simple/goal:

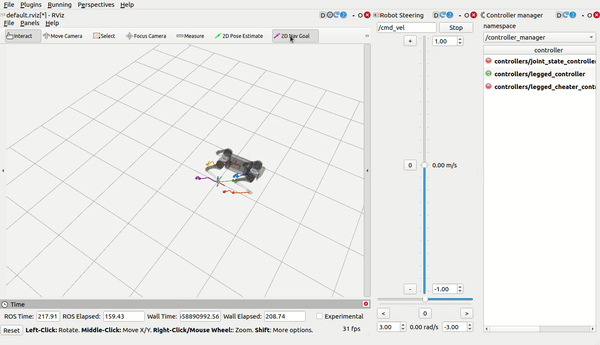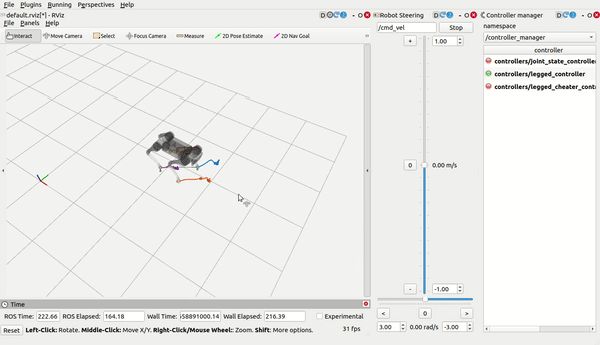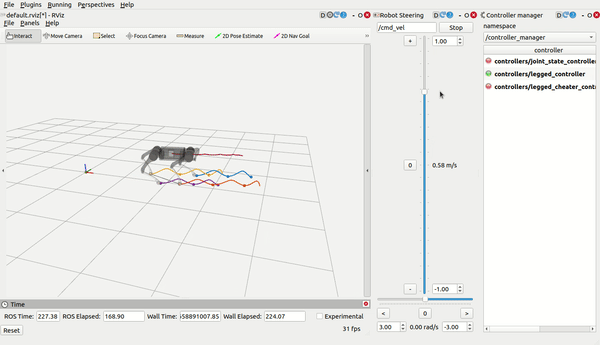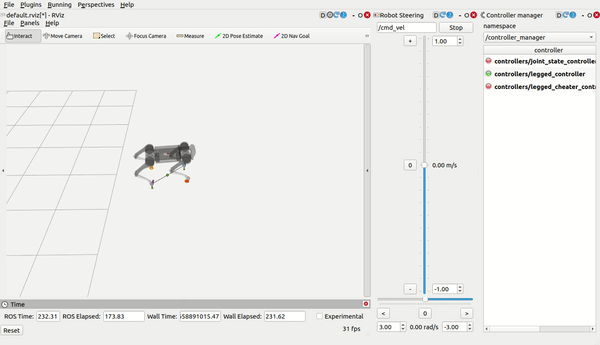
Note

THE GAIT AND THE GOAL ARE COMPLETELY DIFFERENT AND SEPARATED! You don't need to type stance while the robot is lying on the ground with four foot touching the ground; it's completely wrong since the robot is already in the stance gait.
The target_trajectories_publisher is for demonstration. You can combine the trajectory publisher and gait command into a very simple node to add gamepad and keyboard input for different gaits and torso heights and to start/stop controller (by ros service).

Framework

The system framework diagram is shown below.

The robot torso's desired velocity or position goal is converted to state trajectory and then sent to the NMPC;
The NMPC will evaluate an optimized system state and input.
The Whole-body Controller (WBC) figures out the joint torques according to the optimized states and inputs from the NMPC.
The torque is set as a feed-forward term and is sent to the robot's motor controller. Low-gain joint-space position and velocity PD commands are sent to the robot's motors to reduce the shock during foot contact and for better tracking performance.
The NMPC and WBC need to know the current robot state, the base orientation, and the joint state, all obtained directly from the IMU and the motors. Running in the same loop with WBC, a linear Kalman filter[1] estimates the base position and velocity from base orientation, base acceleration, and joint foot position measurements.

Module

The main module of the entire control framework is NMPC and WBC, and the following is only a very brief introduction.

NMPC

The NMPC part solves the following optimization problems at each cycle through the formulation and solving interfaces provided by OCS2:

$$ \begin{split} \begin{cases} \underset{\mathbf u(.)}{\min} \ \ \phi(\mathbf x(t_I)) + \displaystyle \int_{t_0}^{t_I} l(\mathbf x(t), \mathbf u(t), t) , dt \ \text{s.t.} \ \ \mathbf x(t_0) = \mathbf x_0 ,\hspace{11.5em} \text{initial state} \ \ \ \ \ \ \dot{\mathbf x}(t) = \mathbf f(\mathbf x(t), \mathbf u(t), t) \hspace{7.5em} \text{system flow map} \ \ \ \ \ \ \mathbf g_1(\mathbf x(t), \mathbf u(t), t) = \mathbf{0} \hspace{8.5em} \text{state-input equality constraints} \ \ \ \ \ \ \mathbf g_2(\mathbf x(t), t) = \mathbf{0} \hspace{10.5em} \text{state-only equality constraints} \ \ \ \ \ \ \mathbf h(\mathbf x(t), \mathbf u(t), t) \geq \mathbf{0} \hspace{8.5em} \text{inequality constraints} \end{cases}\end{split} $$

For this framework, we defined system state $\mathbf{x}$ and input $\mathbf{u}$ as:

$$ \begin{equation} \mathbf{x}= [\mathbf{h}_{com}^T, \mathbf{q}_b^T, \mathbf{q}_j^T]^T, \mathbf{u} = [\mathbf{f}_c^T, \mathbf{v}_j^T]^T \end{equation} $$

where $\mathbf{h}_{com} \in \mathbb{R}^6$ is the collection of the normalized centroidal momentum, $\mathbf{q}=[\mathbf{q}_b^T, \mathbf{q}_j^T]^T$ is the generalized coordinate. $\mathbf{f}_c \in \mathbb{R}^{12}$ consists of contact forces at four contact points, i.e., four ground reaction forces of the foot. $\mathbf{q}_j$ and $\mathbf{v}_j$ are the joint positions and velocities. While the cost function is simply the quadratic cost of tracking the error of all states and the input, the system dynamics uses centroidal dynamics with the following constraints:

Friction cone;
No motion at the standing foot;
The z-axis position of the swinging foot satisfies the gait-generated curve.

To solve this optimal control problem, a multiple shooting is formulated to transcribe the optimal control problem to a nonlinear program (NLP) problem, and the NLP problem is solved using Sequential Quadratic Programming (SQP). The QP subproblem is solved using HPIPM. For more details [2, 3]

WBC

WBC only considers the current moment. Several tasks are defined in the table above. Each task is the equality constraints or inequality constraints on decision variables. The decision variables of WBC are:

$$ \mathbf{x}_{wbc} = [\ddot{\mathbf{q}}^T, \mathbf{f}_c^T, \mathbf{\tau}^T]^T $$

where $\ddot{\mathbf{q}}$ is acceleration of generalized coordinate, $\mathbf{\tau}$ is the joint torque. The WBC solves the QP problem in the null space of the higher priority tasks' linear constraints and tries to minimize the slacking variables of inequality constraints. This approach can consider the full nonlinear rigid body dynamics and ensure strict hierarchy results. For more details [4].

Deploy and Develop

A1 robot

People with ROS foundation should be able to run through simulation and real machine deployment within a few hours. The following shows some known laboratories that have run through this framework on their own A1 objects. and the time spent The table below shows the labs successfully deploying this repo in their real A1; feel free to open a PR to update it. (because the code they got at the time was not stable, so the spend time cannot represent the their level).

Lab	XPeng Robotics	Unitree	Hybrid Robotics
Spend Time	1 day	-	2 hours

I recommended to use an external computing device such as NUC to run this control framework. The author uses the 11th generation of NUC, and the computing frequency of NMPC can be close to 200Hz.

Your costum rorbots

Deploying this framework to your robot is very simple, the steps are as follows:

Imitate the UnitreeHW class in legged_examples/legged_unitree/legged_unitree_hw , inherit LeggedHW and implement the read() and write() functions of the hardware interface;
Imitate the legged_examples/legged_unitree/legged_unitree_description, write the xarco of the robot and generate the URDF file, note that the names of the joint and link need to be the same as legged_unitree_description.

Reference

[1] T. Flayols, A. Del Prete, P. Wensing, A. Mifsud, M. Benallegue, and O. Stasse, “Experimental evaluation of simple estimators for humanoid robots,” IEEE-RAS Int. Conf. Humanoid Robot., pp. 889–895, 2017, doi: 10.1109/HUMANOIDS.2017.8246977.

[2] J. P. Sleiman, F. Farshidian, M. V. Minniti, and M. Hutter, “A Unified MPC Framework for Whole-Body Dynamic Locomotion and Manipulation,” IEEE Robot. Autom. Lett., vol. 6, no. 3, pp. 4688–4695, 2021, doi: 10.1109/LRA.2021.3068908.

[3] R. Grandia, F. Jenelten, S. Yang, F. Farshidian, and M. Hutter, “Perceptive Locomotion through Nonlinear Model Predictive Control,” (submitted to) IEEE Trans. Robot., no. August, 2022, doi: 10.48550/arXiv.2208.08373.

[4] C. Dario Bellicoso, C. Gehring, J. Hwangbo, P. Fankhauser, and M. Hutter, “Perception-less terrain adaptation through whole body control and hierarchical optimization,” in IEEE-RAS International Conference on Humanoid Robots, 2016, pp. 558–564, doi: 10.1109/HUMANOIDS.2016.7803330.