Awesome

A simple term rewriting system with Wolfram Language's syntax

Inspired by the book Write Yourself a Scheme in 48 Hours. I decide to write myself a simple interpreter of Wolfram Language to learn more about Haskell as well as achieve a deeper understanding about Mathematica, which is the desktop IDE for Wolfram Language.

ScreenShot

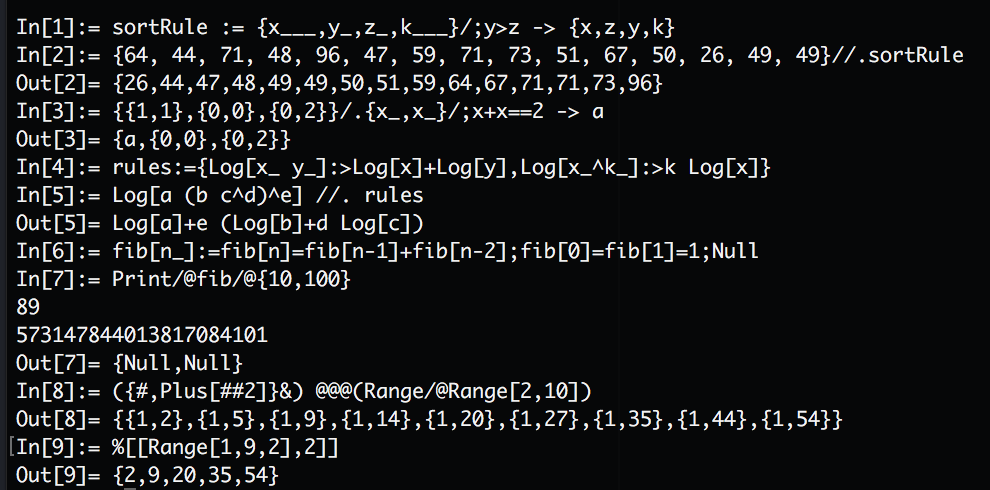
mmaclone

Running (Using Stack)

  git clone https://github.com/jyh1/mmaclone.git
  cd mmaclone/mmaclone
  stack setup
  stack build
  stack exec mmaclone-exe

Prebulid binary files are available on the release page

Features

This interpreter is intended to mimic every exact detail of Wolfram Language, including but not limited to its syntax, semantic, expression structure, evaluation details, etc. (All the scripts below were executed in the REPL session of the mmaclone program)

The program support nearly all Wolfram Language's syntax sugar, infix operators as well as their precedence. E.g., inequality expression chain is parsed to the same AST with Wolfram Language.

In[1]:= FullForm[a==b>=c<=d<e]
Out[1]= Inequality[a,Equal,b,GreaterEqual,c,LessEqual,d]

Some more complicated examples.

In[2]:= FullForm[P@1@2//3]
Out[2]= 3[P[1[2]]]
In[3]:= FullForm[P''''[x]]
Out[3]= Derivative[4][P][x]
In[4]:= FullForm[Hold[(1 ##&)[2]]]
Out[4]= Hold[Function[Times[1,SlotSequence[1]]][2]]

Wolfram Language's powerful pattern matching is also implemented with scrupulous.

(*The famous bubble sort implementation*)
In[1]:= sortRule := {x___,y_,z_,k___}/;y>z -> {x,z,y,k}
In[2]:= {64, 44, 71, 48, 96, 47, 59, 71, 73, 51, 67, 50, 26, 49, 49}//.sortRule
Out[2]= {26,44,47,48,49,49,50,51,59,64,67,71,71,73,96}
(*Symbolic manipulation*)
In[3]:= rules:={Log[x_ y_]:>Log[x]+Log[y],Log[x_^k_]:>k Log[x]}
In[4]:= Log[a (b c^d)^e] //. rules
Out[4]= Log[a]+e (Log[b]+d Log[c])

Currently, the derivative function D is not built-in supported, but you could easily implement one with the powerful pattern matching facilities.

In[5]:= D[a_,x_]:=0
In[6]:= D[x_,x_]:=1
In[7]:= D[a_+b__,x_]:=D[a,x]+D[Plus[b],x]
In[8]:= D[a_ b__,x_]:=D[a,x] b+a D[Times[b],x]
In[9]:= D[a_^(b_), x_]:= a^b(D[b,x] Log[a]+D[a,x]/a b)
In[10]:= D[Log[a_], x_]:= D[a, x]/a
In[11]:= D[Sin[a_], x_]:= D[a,x] Cos[a]
In[12]:= D[Cos[a_], x_]:=-D[a,x] Sin[a]
(*performing derivative*)
In[13]:= D[Sin[x]/x,x]
Out[13]= -x^(-2) Sin[x]+Cos[x] x^(-1)
In[14]:= D[%,x]
Out[14]= -Cos[x] x^(-2)-(-2 x^(-3) Sin[x]+Cos[x] x^(-2))-x^(-1) Sin[x]

Pattern test facility is of the same semantic with `Wolfram Language`'s.

In[15]:= {{1,1},{0,0},{0,2}}/.{x_,x_}/;x+x==2 -> a
Out[15]= {a,{0,0},{0,2}}
In[16]:= {a, b, c, d, a, b, b, b} /. a | b -> x
Out[16]= {x,x,c,d,x,x,x,x}
In[17]:= g[a_*b__]:=g[a]+g[Times[b]]
In[18]:= g[x y z k l]
Out[18]= g[k]+g[l]+g[x]+g[y]+g[z]
In[19]:= q[i_,j_]:=q[i,j]=q[i-1,j]+q[i,j-1];q[i_,j_]/;i<0||j<0=0;q[0,0]=1;Null
In[20]:= q[5,5]
Out[20]= 252

Some more interesting scripts

In[1]:= ((#+##&) @@#&) /@{{1,2},{2,2,2},{3,4}}
Out[1]= {4,8,10}
In[2]:= fib[n_]:=fib[n]=fib[n-1]+fib[n-2];fib[1]=fib[2]=1;Null
In[3]:= fib[100]
Out[3]= 354224848179261915075
In[4]:= fib[1000000000000]
Iteration Limit exceeded, try to increase $IterationLimit
In[5]:= Print/@fib/@{10,100}
55
354224848179261915075
Out[5]= {Null,Null}

For more information please refer to the project wiki (still under construction).

Features that are likely to be added in future versions:

(Some serious design errors are exposed during development, which I consider are inhibiting the project from scaling up. So currently my primary focus would be on refactor rather than adding new features/functions)

More mathematical functions (Sin, Cos, Mod etc...)
Arbitrary precision floating arithmetic using GMP(GNU Multiple Precision Arithmetic Library), currently arbitrary integer, double and rational number are supported.
More built-in functions (Level, Import, Derivativeetc...)
More sophisticated pattern matching

~~head specification (of the form Blank[Head], currently it only support list type)~~(Implemented)
~~Pattern Test~~(Implemented)
~~BlankSequence, BlankNullSequence~~(Implemented)
Other pattern matching expression, like Verbatim, Longest