Awesome
Quick Start Guide for mexBBFMM2D, a MATLAB interface for Black Box Fast Multipole Method (BBFMM2D)
==========
Function
Perform fast (linear) multiplication of a kernel matix Q with a vector or matrix: P = QH
Overview
The Fast Multipole Method (FMM) is an algorithm that performs fast multiplication of an N x N dense matrix Q(x,y) where N is the number of unknown values at points (x,y) in a 2D domain, with a matrix H of size N x m (N>>m). The direct multiplication approach has complexity O(N^2), while the BBFMM2D has linear complexity O(N). As an example, for a matrix of size 10,000x10,000 multiplied to 10,000 x 100, the BBFMM2D takes 1.4 seconds, while the direct approach takes 8.1 seconds, on a single processor laptop. The table below shows computation time on a single core CPU.
| N | Time in seconds |
|---|---|
| 10,000 | 1.4 |
| 100,000 | 11.4 |
| 1,000,000 | 126.2 |
BBFMM2D performs the multiplication by an approximation that relies on Chebyshev interpolation. For details about the method please see Fong and Darve, 2009. The method has an approximation error that can be controlled by input parameters, which can be adjusted depending on the accuracy required. The package BBFMM2D is written in C++ (https://github.com/sivaramambikasaran/BBFMM2D). mexBBFMM2D provides a MATLAB interface for the package BBFMM2D.
Disclaimer
This is a quick-start guide with instructions on how to set up and use mexBBFMM2D in MATLAB, with an example m-file that can be used to perform matrix-vector and matrix-matrix multiplication. A reasonably good knowledge of MATLAB is assumed and minimal understanding of the FMM theory is needed.
For a more involved description of the code and the method please see here, and for a full description of the algorithm see [Fong and Darve 2006] in section Reference.
In this guide, we will use the example of the multiplication of a Gaussian covariance matrix Q (termed as Gaussian kernel) with a matrix H. The method can also be applied for other smooth kernels (see section Appendix).
Quick start guide
Step 1: Download the code and supporting software
Step 1a: Check if you have MEX and MATLAB Symbolic Math Toolbox set up in Matlab
This package relies on MATLAB MEX functions and MATLAB Symbolic Math Toolbox. In order to use MEX functions, you should setup mex.
Setup MEX by typing the following MATLAB command
mex -setup
Attention Mac users: If you have upgraded to Xcode 7, see Answer by MathWorks Support Team on 28 Dec 2015.
Once mex is set up successfully, to ensure that MEX is installed, try the following commands:
copyfile([matlabroot,'/extern/examples/mex/arraySize.c'],'./','f')
mex -v arraySize.c
arraySize(5000)
The last two lines of the screen output should read
Dimensions: 5000x5000
Size of array in kilobytes: 24414
If you have trouble with setting up mex, see Trouble Shooting.md
Step 1b: Download the code from https://github.com/judithyueli/mexBBFMM2D/archive/master.zip
A folder called mexBBFMM2D-master will be downloaded. Copy the folder mexBBFMM2D-master to your specific working directory. In MATLAB, set the current folder to be the directory where the downloaded folder was copied. You will see the folders
BBFMM2D\ and Eigen\, as well as an m-file called (compilemex.m) and an example m-file (example_case1.m) that we will use in this quick start quide. These m-files will be used to compile, set-up, test and use the BBFMM2D. The user only needs to change these m-files. No modifications will be needed to the contents of the folder BBFMM2D which includes the c++ source code.
Note: For Step 2 you have to operate in the main directory of mexBBFMM2D, which contains make.m, For Step 3 or 4, you can call the generated MEX-files (e.g., case1.mexmaci64) by moving them to your own working directory, or add the main directory of mexBBFMM2D to the path.
Step 2: Compile the MEX file
A. Open file compilemex.m
B. Define your kernel function, e.g. kernel = exp(-sqrt(r^0.5)/30);
C. Give your BBFMM2D case a name, e.g. case1
syms r % define independent variable as a symbolic variable
kernel = exp(-sqrt(r^0.5)/30); % define kernel using symbolic expression (has to be a function of the symbolic variable!)
outputfile = 'case1';
Run compilemex.m. It will compile the source code and generate a MEX-file with your provied name (e.g. case1.mexmaci64). The extension (.mexmaci64) will depend on your platform.
NOTE!! Recompile the MEX-file (step 2) when the kernel function is changed.
Step 3: Run example
Example description:
This example is for a 2D regular grid of size 100 x 100. The covariance matrix Q of this grid has size 10,000 x 10,000. mexBBFMM2D will perform fast multiplication of Q (the (i,j)-th entry of Q is kernel(xi, xj)) with a matrix H given by ones(10000,100).
Open example_case1.m to inspect the commands. The first part sets up the grid and other parameters required by mexBBFMM2D that will be explained in detail below.
Change the ExecName to the name you used in compilemex for your executable.
Then, choose whether you want to run mexBBFMM2D in Testing Mode or in Execution mode. In Testing Mode, the code multiplies Q and H with both fast (BBFMM2D) and direct method. It outputs the runnting time for each method as well as the relative error. This mode is useful when one wants to determine how many Chebyshev nodes (nCheb) to use for a desired accuracy. It will take a long time because the direct multiplication is also performed. Caution! Do not use for large matrices because direct multiplication will take for ever. In Application Mode, the code uses BBFMM2D only and does not compare with the direct approach. This mode should be used for large problems.
The rest of the example defines the grid information, the H matrix and number of Chebyshev nodes, as well as a PrintFlag which can be set to false for limited printout.
To run the example, run the command:
example_case1
The mfile that runs BBFMM2D is runmexBBFMM2D.m and no changes are needed in this m-file. Everything is defined in the example_case1.m
QH = runmexBBFMM2D(xloc, yloc,H,nCheb,PrintFlag,ExecName,TestingMode);
Input:
xloc, yloc: These are the x and y coordinates of grid points, respectively. [xloc(i), yloc(i)] gives the location of the i-th point. For example for a 2x2 grid in [0,1] it would be xloc=[0 0 1 1]’ and yloc=[0 1 0 1]’. The grid does not have to be regular or structured.
H: the matrix we want to multiply Q with (QH)
nCheb: number of Chebyshev nodes per dimension (larger nCheb gives higher accuracy, but higher computational cost), integers between 4 and 6 are suggested. Try starting with 4 and increase to achieve desirable accuracy.
PrintFlag: flag for printing the output details: 1 for print, and 0 for no print.
Output:
QH: the product of Q and H as given by BBFMM2D
Example results for QH with nCheb=4,5,6. Large nCheb will give greater accuracy but more time consuming.
| nCheb | Relative Error | Time(s) with BBFMM2D | Time(s) with direct multiplication |
|---|---|---|---|
| 4 | 4.45E-08 | 0.67s | 8.01s |
| 5 | 1.66E-09 | 0.85s | 8.06s |
| 6 | 3.20E-10 | 1.44s | 8.34s |
Relative error = norm (QHfast - QH) / norm(QH)
Step 4: Run you own example
- Determine your kernel type and compile the mex file with a name of your choice, e.g.,
expfun.mex(step 2) - Add
expfun.mexto your path, or move it to your current directory - Set up your grid coordinates in two vectors
locxandlocyand the right multiplierH(seeexample_case1.m) - Run mexBBFMM2D in testing mode to determine number of Chebyshev nodes
TestingMode = true;
ExecName = 'expfun';
QH = runmexBBFMM2D(xloc, yloc,H,nCheb,PrintFlag,ExecName,TestingMode);
- Run mexBBFMM2D in application mode for your own example.
TestingMode = false;
ExecName = 'expfun';
QH = runmexBBFMM2D(xloc, yloc,H,nCheb,PrintFlag,ExecName,TestingMode);
APPENDIX<a name="ref_app"></a>
Kernel Options
r : distance between two points
L : length scale parameter
\sigma^2: variance parameter
Example of kernel type:
-
Gaussian kernel
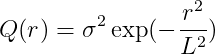 -
Exponential kernel
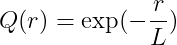 -
Logrithm kernel
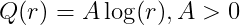 -
Linear kernel
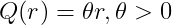 -
Power kernel
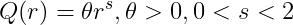
This package uses:
Reference:<a name="ref"></a>
- Sivaram Ambikasaran, Judith Yue Li, Peter K. Kitanidis, Eric Darve, Large-scale stochastic linear inversion using hierarchical matrices, Computational Geosciences, December 2013, Volume 17, Issue 6, pp 913-927 link
- Judith Yue Li, Sivaram Ambikasaran, Eric F. Darve, Peter K. Kitanidis, A Kalman filter powered by H2-matrices for quasi-continuous data assimilation problems link
- Saibaba, A., S. Ambikasaran, J. Li, P. Kitanidis, and E. Darve (2012), Application of hierarchical matrices to linear inverse problems in geostatistics, OGST Revue d’IFP Energies Nouvelles, 67(5), 857–875, doi:http://dx.doi.org/10.2516/ogst/2012064. link
- Fong, W., and E. Darve (2009), The black-box fast multipole method, Journal of Computational Physics, 228(23), 8712–8725.link