Home

Awesome

<p align="center"> <img src="https://deephypergraph.com/logo_DHG.png" height="200"> </p>

Release version PyPI version Website Build Status Documentation Status Downloads Visits Badge license

<!-- [![Code style: Black](https://img.shields.io/badge/code%20style-Black-000000.svg)](https://github.com/psf/black) --> <!-- [![Supported Python versions](https://img.shields.io/pypi/pyversions/dhg)](https://pypi.org/project/dhg/) -->

Website | Documentation | Tutorials | 中文文档 | Official Examples | Discussions

News

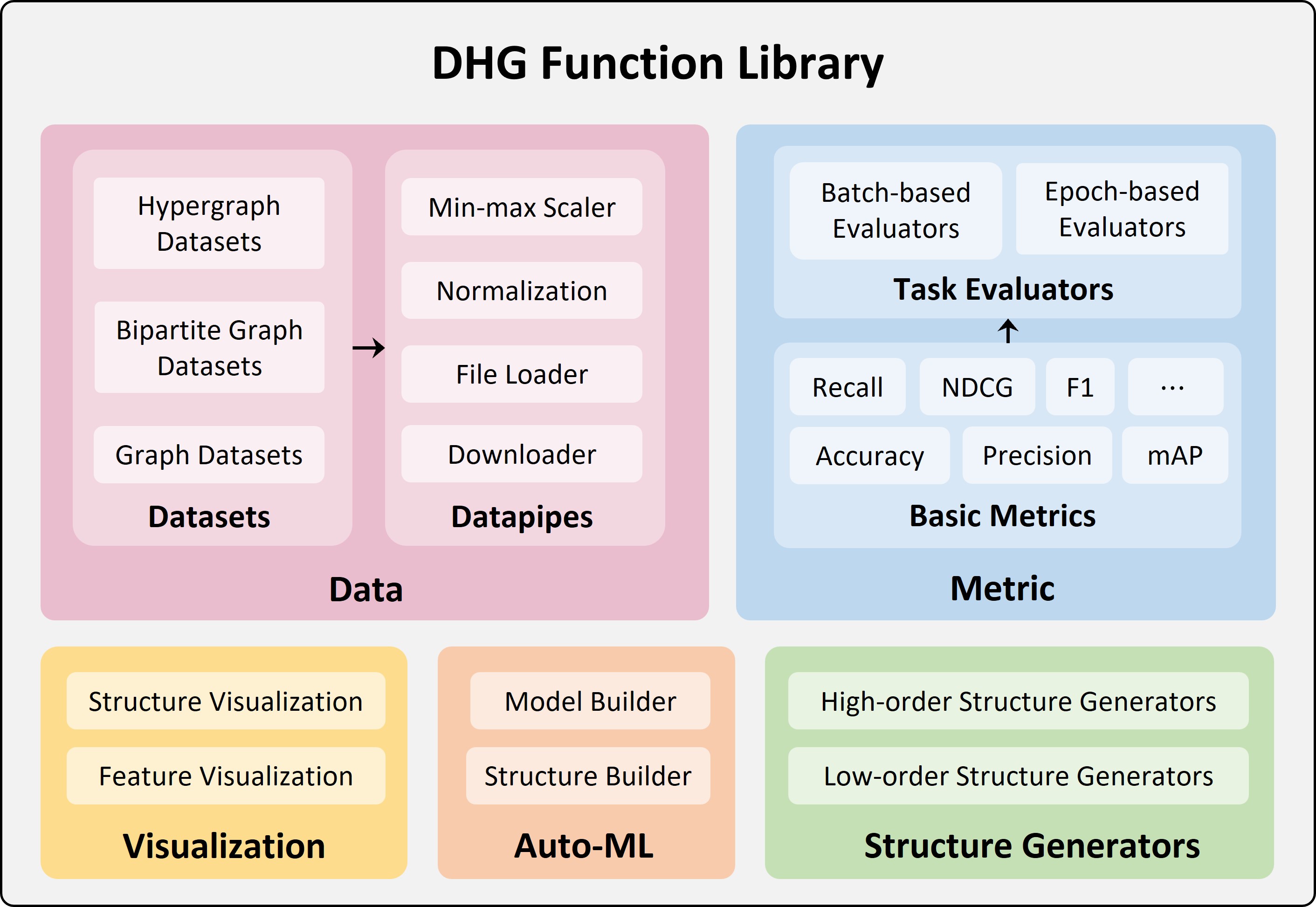
DHG (DeepHypergraph) is a deep learning library built upon PyTorch for learning with both Graph Neural Networks and Hypergraph Neural Networks. It is a general framework that supports both low-order and high-order message passing like from vertex to vertex, from vertex in one domain to vertex in another domain, from vertex to hyperedge, from hyperedge to vertex, from vertex set to vertex set.

It supports a wide variety of structures like low-order structures (graph, directed graph, bipartite graph, etc.), high-order structures (hypergraph, etc.). Various spectral-based operations (like Laplacian-based smoothing) and spatial-based operations (like message psssing from domain to domain) are integrated inside different structures. It provides multiple common metrics for performance evaluation on different tasks. Many state-of-the-art models are implemented and can be easily used for research. We also provide various visualization tools for both low-order structures and high-order structures.

In addition, DHG's dhg.experiments module (that implements Auto-ML upon Optuna) can help you automatically tune the hyper-parameters of your models in training and easily outperforms the state-of-the-art models.

Framework of DHG Structures

Framework of DHG Function Library

Highlights

Installation

Current, the stable version of DHG is 0.9.4. You can install it with pip as follows:

pip install dhg

You can also try the nightly version (0.9.5) of DHG library with pip as follows:

pip install git+https://github.com/iMoonLab/DeepHypergraph.git

Nightly version is the development version of DHG. It may include the lastest SOTA methods and datasets, but it can also be unstable and not fully tested. If you find any bugs, please report it to us in GitHub Issues.

Quick Start

Visualization

You can draw the graph, hypergraph, directed graph, and bipartite graph with DHG's visualization tool. More details see the Tutorial

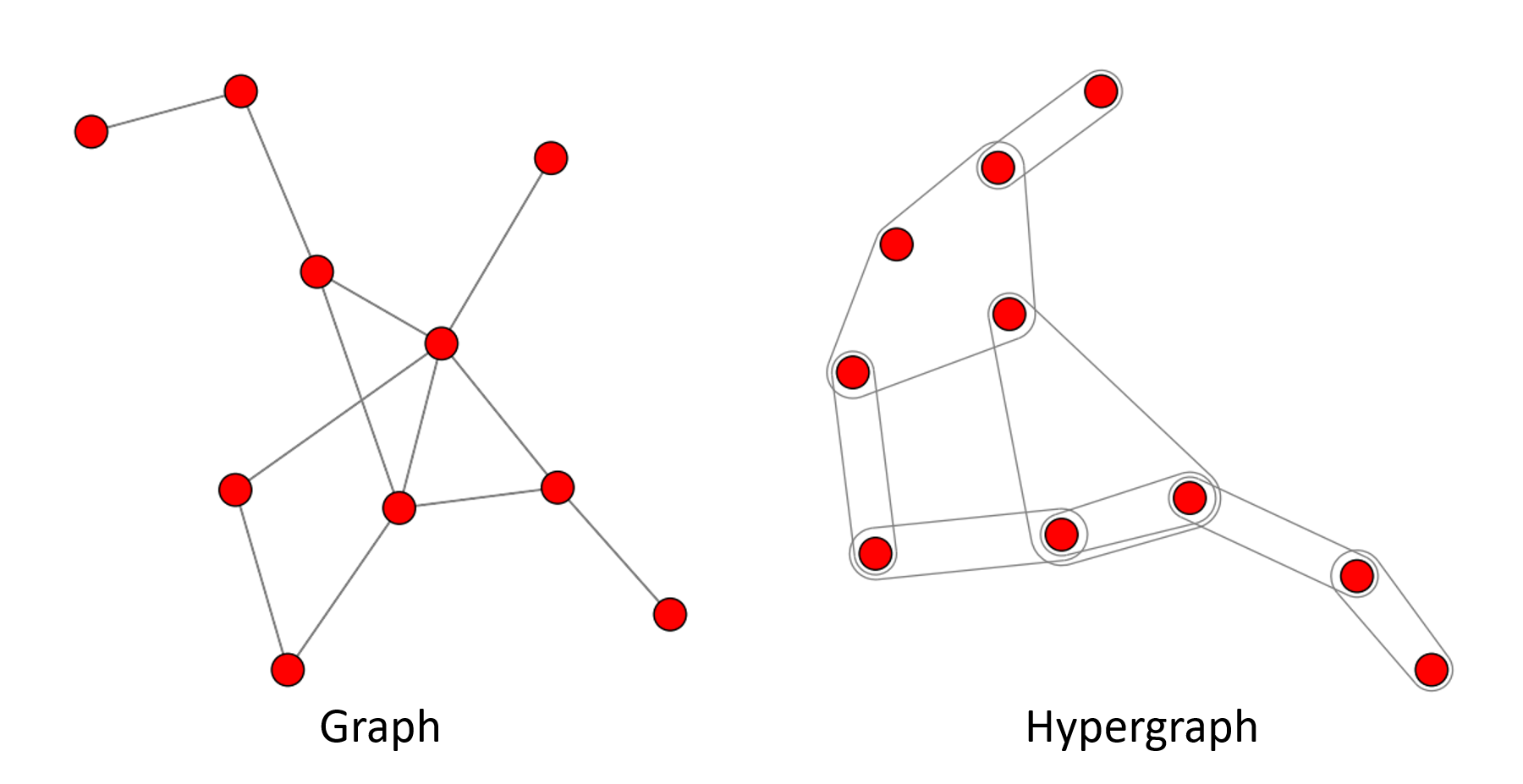
Visualization of graph and hypergraph

import matplotlib.pyplot as plt
import dhg
# draw a graph
g = dhg.random.graph_Gnm(10, 12)
g.draw()
# draw a hypergraph
hg = dhg.random.hypergraph_Gnm(10, 8)
hg.draw()
# show figures
plt.show()

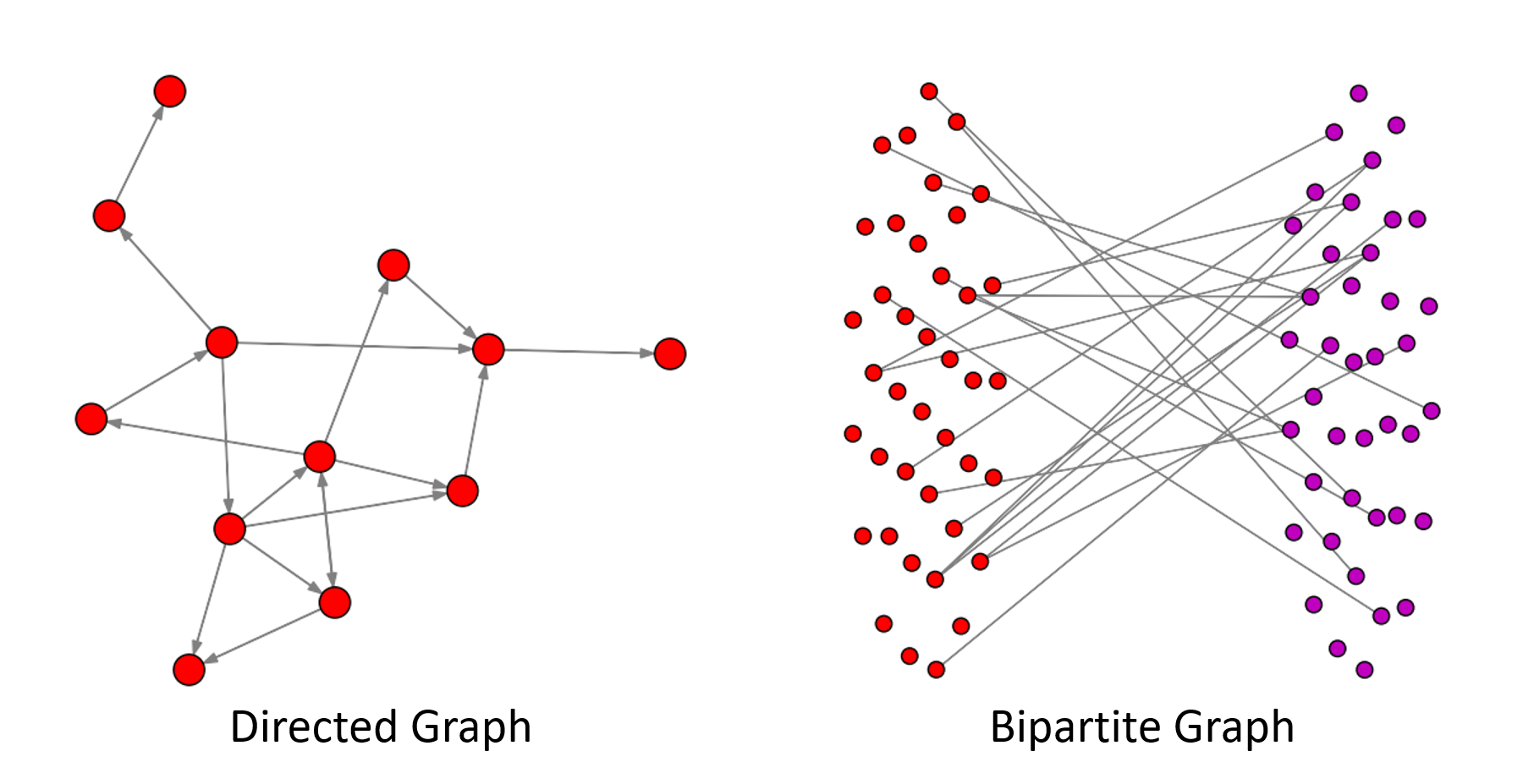
Visualization of directed graph and bipartite graph

import matplotlib.pyplot as plt
import dhg
# draw a directed graph
g = dhg.random.digraph_Gnm(12, 18)
g.draw()
# draw a bipartite graph
g = dhg.random.bigraph_Gnm(30, 40, 20)
g.draw()
# show figures
plt.show()

Learning on Low-Order Structures

On graph structures, you can smooth a given vertex features with GCN's Laplacian matrix by:

import torch
import dhg
g = dhg.random.graph_Gnm(5, 8)
X = torch.rand(5, 2)
X_ = g.smoothing_with_GCN(X)

On graph structures, you can pass messages from vertex to vertex with mean aggregation by:

import torch
import dhg
g = dhg.random.graph_Gnm(5, 8)
X = torch.rand(5, 2)
X_ = g.v2v(X, aggr="mean")

On directed graph structures, you can pass messages from vertex to vertex with mean aggregation by:

import torch
import dhg
g = dhg.random.digraph_Gnm(5, 8)
X = torch.rand(5, 2)
X_ = g.v2v(X, aggr="mean")

On bipartite graph structures, you can smoothing vertex features with GCN's Laplacian matrix by:

import torch
import dhg
g = dhg.random.bigraph_Gnm(3, 5, 8)
X_u, X_v = torch.rand(3, 2), torch.rand(5, 2)
X = torch.cat([X_u, X_v], dim=0)
X_ = g.smoothing_with_GCN(X, aggr="mean")

On bipartite graph structures, you can pass messages from vertex in U set to vertex in V set by mean aggregation by:

import torch
import dhg
g = dhg.random.bigraph_Gnm(3, 5, 8)
X_u, X_v = torch.rand(3, 2), torch.rand(5, 2)
X_u_ = g.v2u(X_v, aggr="mean")
X_v_ = g.u2v(X_u, aggr="mean")

Learning on High-Order Structures

On hypergraph structures, you can smooth a given vertex features with HGNN's Laplacian matrix by:

import torch
import dhg
hg = dhg.random.hypergraph_Gnm(5, 4)
X = torch.rand(5, 2)
X_ = hg.smoothing_with_HGNN(X)

On hypergraph structures, you can pass messages from vertex to hyperedge with mean aggregation by:

import torch
import dhg
hg = dhg.random.hypergraph_Gnm(5, 4)
X = torch.rand(5, 2)
Y_ = hg.v2e(X, aggr="mean")

Then, you can pass messages from hyperedge to vertex with mean aggregation by:

X_ = hg.e2v(Y_, aggr="mean")

Or, you can pass messages from vertex set to vertex set with mean aggregation by:

X_ = hg.v2v(X, aggr="mean")

Examples

Building the Convolution Layer of GCN

class GCNConv(nn.Module):
    def __init__(self,):
        super().__init__()
        ...
        self.reset_parameters()

    def forward(self, X: torch.Tensor, g: dhg.Graph) -> torch.Tensor:
        # apply the trainable parameters ``theta`` to the input ``X``  
        X = self.theta(X)
        # smooth the input ``X`` with the GCN's Laplacian
        X = g.smoothing_with_GCN(X)
        X = F.relu(X)
        return X

Building the Convolution Layer of GAT

class GATConv(nn.Module):
    def __init__(self,):
        super().__init__()
        ...
        self.reset_parameters()

    def forward(self, X: torch.Tensor, g: dhg.Graph) -> torch.Tensor:
        # apply the trainable parameters ``theta`` to the input ``X``
        X = self.theta(X)
        # compute attention weights for each edge
        x_for_src = self.atten_src(X)
        x_for_dst = self.atten_dst(X)
        e_atten_score = x_for_src[g.e_src] + x_for_dst[g.e_dst]
        e_atten_score = F.leaky_relu(e_atten_score).squeeze()
        # apply ``e_atten_score`` to each edge in the graph ``g``, aggragete neighbor messages
        #  with ``softmax_then_sum``, and perform vertex->vertex message passing in graph 
        #  with message passing function ``v2v()``
        X = g.v2v(X, aggr="softmax_then_sum", e_weight=e_atten_score)
        X = F.elu(X)
        return X

Building the Convolution Layer of HGNN

class HGNNConv(nn.Module):
    def __init__(self,):
        super().__init__()
        ...
        self.reset_parameters()

    def forward(self, X: torch.Tensor, hg: dhg.Hypergraph) -> torch.Tensor:
        # apply the trainable parameters ``theta`` to the input ``X``
        X = self.theta(X)
        # smooth the input ``X`` with the HGNN's Laplacian
        X = hg.smoothing_with_HGNN(X)
        X = F.relu(X)
        return X

Building the Convolution Layer of HGNN $^+$

class HGNNPConv(nn.Module):
    def __init__(self,):
        super().__init__()
        ...
        self.reset_parameters()

    def forward(self, X: torch.Tensor, hg: dhg.Hypergraph) -> torch.Tensor:
        # apply the trainable parameters ``theta`` to the input ``X``
        X = self.theta(X)
        # perform vertex->hyperedge->vertex message passing in hypergraph
        #  with message passing function ``v2v``, which is the combination
        #  of message passing function ``v2e()`` and ``e2v()``
        X = hg.v2v(X, aggr="mean")
        X = F.relu(X)
        return X

Datasets

Currently, we have added the following datasets:

Metrics

Classification Metrics

Recommender Metrics

Retrieval Metrics

Implemented Models

On Low-Order Structures

On High-Order Structures

Citing

If you find DHG is useful in your research, please consider citing:

@article{gao2022hgnn,
  title={HGNN $\^{}+ $: General Hypergraph Neural Networks},
  author={Gao, Yue and Feng, Yifan and Ji, Shuyi and Ji, Rongrong},
  journal={IEEE Transactions on Pattern Analysis and Machine Intelligence},
  year={2022},
  publisher={IEEE}
}

@inproceedings{feng2019hypergraph,
  title={Hypergraph neural networks},
  author={Feng, Yifan and You, Haoxuan and Zhang, Zizhao and Ji, Rongrong and Gao, Yue},
  booktitle={Proceedings of the AAAI conference on artificial intelligence},
  volume={33},
  number={01},
  pages={3558--3565},
  year={2019}
}

The DHG Team

DHG is developed by DHG's core team including Yifan Feng, Xinwei Zhang, Jielong Yan, Xiangmin Han, Yue Gao, and Qionghai Dai. It is maintained by the iMoon-Lab, Tsinghua University. You can contact us at email.

License

DHG uses Apache License 2.0.