Awesome

Equalized Odds and Calibration

We test two post-processing definitions of non-discrimination:

Equalized Odds - from "Equality of Opportunity in Supervised Learning" - [1]
A calibrated relaxation of Equalized Odds - from "On Fairness and Calibration" - [2]

Given two demographic groups, equalized odds aims to ensure that no error rate disproportionately affects any group. In other words, both groups should have the same false-positive rate, and both groups should have the same false-negative rate.

We would like to achieve this definition of non-discrimination while maintaining calibrated probability estimates. However, achieving both of these goals is impossible [3]. Therefore, we seek to maintain calibration while matching a single cost constraint. The equal cost constraint can be:

Equal false-negative rates between the two groups
Equal false-positive rates between the two groups
Equal weighted combination of the error rates between the two groups

How to use

The files eq_odds.py and calib_eq_odds.py contain post-processing methods for achieving these two notions of non-discrimination. Each file expects as input the predictions (and ground-truth labels) from an already-trained model. See the demos in each file for example usage.

Metrics

To measure false-negative or false-positive discrimination, it is enough to check the difference in error rates between groups. To measure calibration, we can compare the average model score with the population's base rate. A necessary (but not sufficient) condition for calibration is that the average model score should match the base rate.

For example:

Calib. equalized odds group 0 model:
Accuracy:    0.808
F.P. cost:    0.427
F.N. cost:    0.191
Base rate:    0.701
Avg. score:    0.695

Calib. equalized odds group 1 model:
Accuracy:    0.929
F.P. cost:    0.432
F.N. cost:    0.075
Base rate:    0.888
Avg. score:    0.870

These two models are (probably) calibrated, and have equal false-positive costs. However, they have different false-negative costs.

Equalized odds group 0 model:
Accuracy:    0.825
F.P. cost:    0.388
F.N. cost:    0.180
Base rate:    0.706
Avg. score:    0.693

Equalized odds group 1 model:
Accuracy:    0.830
F.P. cost:    0.432
F.N. cost:    0.179
Base rate:    0.895
Avg. score:    0.781

These two models match both error rates. However, they are not calibrated.

We can also visualize non-discrimination by plotting models on the false-positive/false-negative error plane:

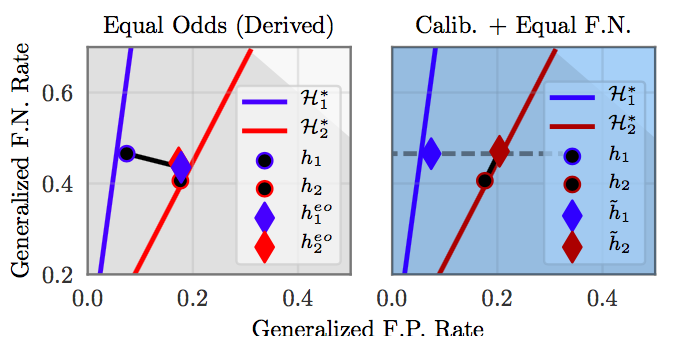
FP-FN Plane

Here, the red and blue lines represent the sets of possible calibrated classifiers for both groups. The black dots represent the original (discriminatory) classifiers for both groups. On the left, we apply Equalized Odds post processing (diamonds). This matches the error rates: however the classifiers no longer live on the calibrated classifier lines. On the right, we apply the calibrated relaxation (calibration and equal false negative rates). This matches the false-negative error rates, and the classifiers remain calibrated. However, they have different false-positive rates.

Experiments in the paper

Income prediction experiment

We wish to ensure that income prediction doesn't discriminate across genders. In our relaxation, we aim to match the false-negative rate between the two groups.

The model scores come from a MLP trained on the UCI heart dataset.

python eq_odds.py data/income.csv
python calib_eq_odds.py data/income.csv fnr

Health prediction experiment

We wish to ensure heart health predictions don't discriminate across age groups. In our relaxation, we aim to match a weighted error combination.

The model scores come from a random forest trained on the UCI heart dataset.

python eq_odds.py data/health.csv
python calib_eq_odds.py data/health.csv weighted

Criminal recidivism prediction experiment

We wish to ensure that criminal recidivism predictions don't discriminate across race. In our relaxation, we aim to match the false-negative rates.

The model scores are actual scores taken from the COMPAS risk assessment tool.

python eq_odds.py data/health.csv
python calib_eq_odds.py data/health.csv weighted

References

[1] Hardt, Moritz, Eric Price, and Nati Srebro. "Equality of opportunity in supervised learning." In NIPS (2016).

[2] Pleiss, Geoff, Manish Raghavan, Felix Wu, Jon Kleinberg, and Kilian Q. Weinberger. "On Fairness and Calibration." In NIPS (2017).

[3] Kleinberg, Jon, Sendhil Mullainathan, and Manish Raghavan. "Inherent trade-offs in the fair determination of risk scores." In ITCS (2017).