Home

Awesome

EFANNA: an Extremely Fast Approximate Nearest Neighbor search Algorithm framework based on kNN graph

EFANNA is a flexible and efficient library for approximate nearest neighbor search (ANN search) on large scale data. It implements the algorithms of our paper EFANNA : Extremely Fast Approximate Nearest Neighbor Search Algorithm Based on kNN Graph.
EFANNA provides fast solutions on both approximate nearest neighbor graph construction and ANN search problems. EFANNA is also flexible to adopt all kinds of hierarchical structure for initialization, such as random projection tree, hierarchical clustering tree, multi-table hashing and so on.

What's new

Benchmark data set

ANN search performance

The performance was tested without parallelism.

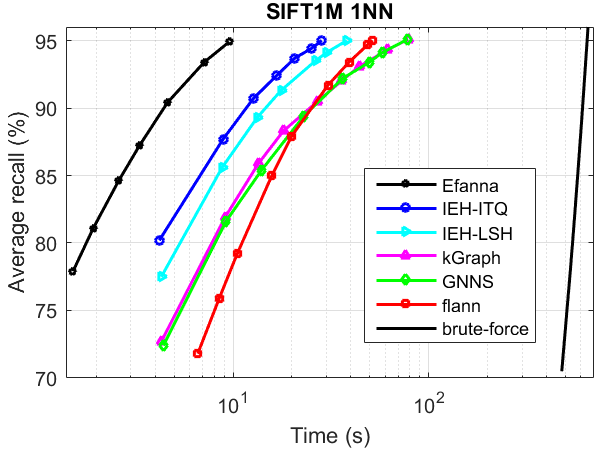
SIFT1nn
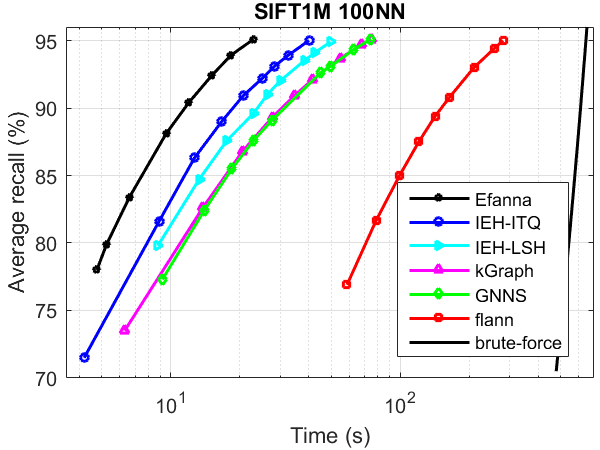
SIFT100nn
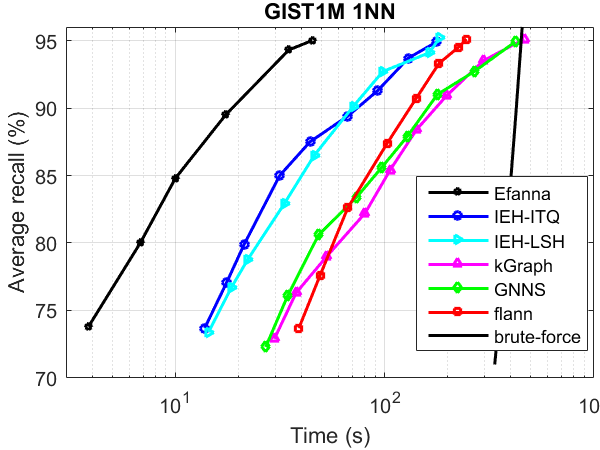
GIST1nn
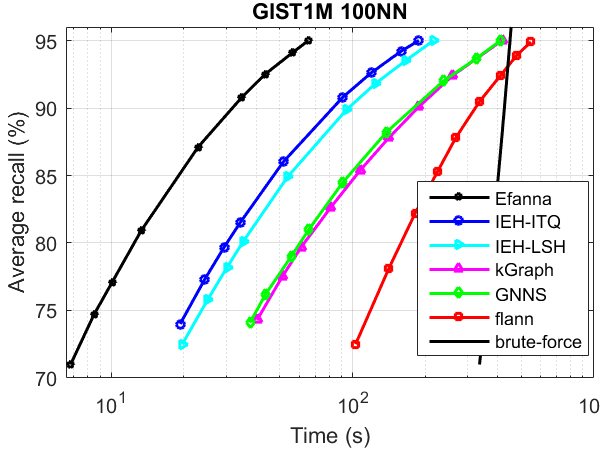
GIST100nn
Compared Algorithms:

kNN Graph Construction Performance

The performance was tested without parallelism.

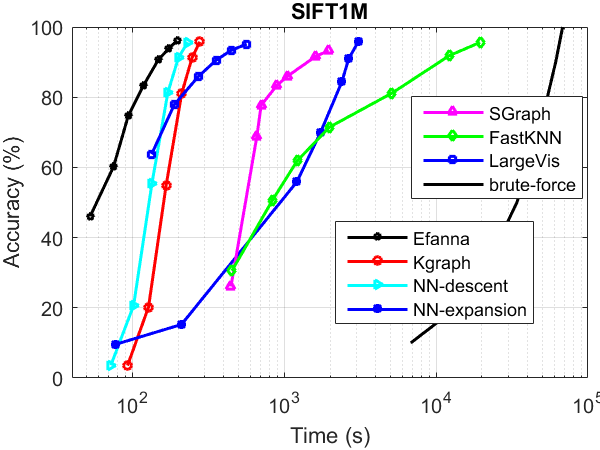
SIFT1nnGraph
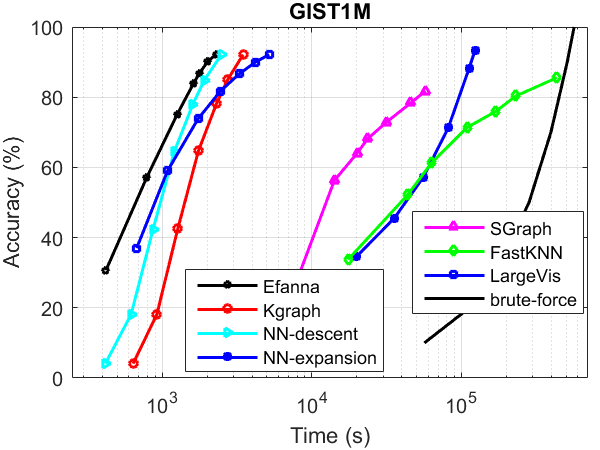
SIFT100nnGraph

Compared Algorithms:

How To Complie

Go to the root directory of EFANNA and make.

cd efanna/
make

How To Use

EFANNA uses a composite index to carry out ANN search, which includes an approximate kNN graph and a number of tree structures. They can be built by this library as a whole or seperately.

You may build the kNN graph seperately for other use, like other graph based machine learning algorithms.

Below are some demos.

Meaning of the parameters(from left to right):

sift_base.fvecs -- database points  
sift.graph -- graph built by EFANNA   

8 -- number of trees used to build the graph (larger is more accurate but slower)   
8 -- conquer-to-depeth(smaller is more accurate but slower)   
8 -- number of iterations to build the graph 
 
30 -- L (larger is more accurate but slower, no smaller than K)  
25 -- check (larger is more accurate but slower, no smaller than K)  
10 -- K, for KNN graph   
10 -- S (larger is more accurate but slower)

See our paper or user manual for more details about the parameters and interfaces.

Output format

The file format of approximate kNN graph and ANN search results are the same.
Suppose the database has N points, and numbered from 0 to N-1. You want to build an approximate kNN graph. The graph can be regarded as a N * k Matrix. The saved kNN graph binary file saves the matrix by row. The first 4 bytes of each row saves the int value of k, next 4 bytes saves the value of M and next 4 bytes saves the float value of the norm of the point. Then it follows k*4 bytes, saving the indices of the k nearest neighbors of respective point. The N rows are saved continuously without seperating characters.

Similarly, suppose the query data has n points, numbered 0 to n-1. You want EFANNA to return k nearest neighbors for each query. The result file will save n rows like the graph file. It saves the returned indices row by row. Each row starts with 4 bytes recording value of k, and follows k*4 bytes recording neighbors' indices.

Input of EFANNA

Because there is no unified format for input data, users may need to write input function to read your own data. You may imitate the input function in our sample code (sample/efanna_efanna_index_buildgraph.cc) to load the data into our matrix.

To use SIMD instruction optimization, you should pay attention to the data alignment problem of SSE / AVX instruction.

Compare with EFANNA without parallelism and SSE/AVX instructions

To disable the parallelism, there is no need to modify the code. Simply

    export OMP_NUM_THREADS=1

before you run the code. Then the code will only use one thread. This is a very convenient way to control the number of threads used.

To disable SSE/AVX instructions, you need to modify samples/xxxx.cc, find the line

    FIndex<float> index(dataset, new L2DistanceAVX<float>(), efanna::KDTreeUbIndexParams(true, trees ,mlevel ,epochs,checkK,L, kNN, trees, S));

Change L2DistanceAVX to L2Distance and build the project. Now the SSE/AVX instructions are disabled. If you want to try SSE instead of AVX, try L2DistanceSSE

Parameters to get the Fig. 4/5 (10-NN approximate graph construction) in our paper

SIFT1M:

    ./efanna_index_buildgraph sift_base.fvecs sift.graph 8 8 0 20 10 10 10
    ./efanna_index_buildgraph sift_base.fvecs sift.graph 8 8 1 20 10 10 10
    ./efanna_index_buildgraph sift_base.fvecs sift.graph 8 8 2 20 10 10 10
    ./efanna_index_buildgraph sift_base.fvecs sift.graph 8 8 3 20 10 10 10
    ./efanna_index_buildgraph sift_base.fvecs sift.graph 8 8 5 20 10 10 10
    ./efanna_index_buildgraph sift_base.fvecs sift.graph 8 8 6 20 20 10 10
    ./efanna_index_buildgraph sift_base.fvecs sift.graph 8 8 6 20 30 10 10

GIST1M:

    ./efanna_index_buildgraph gist_base.fvecs gist.graph 8 8 2 30 30 10 10
    ./efanna_index_buildgraph gist_base.fvecs gist.graph 8 8 3 30 30 10 10
    ./efanna_index_buildgraph gist_base.fvecs gist.graph 8 8 4 30 30 10 10
    ./efanna_index_buildgraph gist_base.fvecs gist.graph 8 8 5 30 30 10 10
    ./efanna_index_buildgraph gist_base.fvecs gist.graph 8 8 6 30 30 10 10
    ./efanna_index_buildgraph gist_base.fvecs gist.graph 8 8 7 30 30 10 10
    ./efanna_index_buildgraph gist_base.fvecs gist.graph 8 8 10 30 40 10 10

Acknowledgment

Our code framework imitates Flann to make it scalable, and the implemnetation of NN-descent is taken from Kgraph. They proposed the NN-descent algorithm. Many thanks to them for inspiration.

What to do