Home

Awesome

GrUMPy 0.95

DOI

Graphics for Understanding Mathematical Programming in Python (GrUMPy) is a Python library for visualizing various aspects of mathematical programming, including visualizations of the branch-and process, branch-and-bound trees, polyhedra, cutting plane methods, etc. The goal is clarity in implementation rather than efficiency. Most methods have an accompanying visualization and are thus appropriate for use in the classroom.

Documentation for the API is here:

https://coin-or.github.io/GrUMPy

Pypi download page is here:

https://pypi.python.org/pypi/coinor.grumpy

See below for brief documentation of usage

Installation Notes

To install, do:

pip install coinor.grumpy
  1. GrUMPy depends on GiMPy, which will be automatically installed as part of the setup. However, in order for GiMPy to visualize the branch-and-bound tree, it's necessary to install GraphViz and choose one of these additional methods for display:

It is also possible to typeset labels in LaTex and to output the graph in LaTex format using dot2tex (Warning: recent versions of dot2tex have not perfectly, your mileage may vary). After installing dot2tex, this can be done by simply calling the method write(basename='fileName', format='dot'), and then doing dot2tex --tmath fileName.dot or by calling set_display_mode('dot2tex') and then display() as usual. At the moment, the latter only seems to work with version 2.9.0dev available here. For the former method, just using easy_install dot2tex should work fine.

  1. GrUMPy also creates some visualizations with gnuplot. For tips on installing gnuplot, see below.
  2. GrUMPy can also visualize 2D polyhedra with the installation of pypolyhedron, which can be install with pip install pypolyhedron

Additional Notes for Windows Installation

Additional Notes for Linux Installation

Additional Notes for OS X Users

Examples of Visualizations

Branch and bound tree

Figure 1 made with GrUMPy

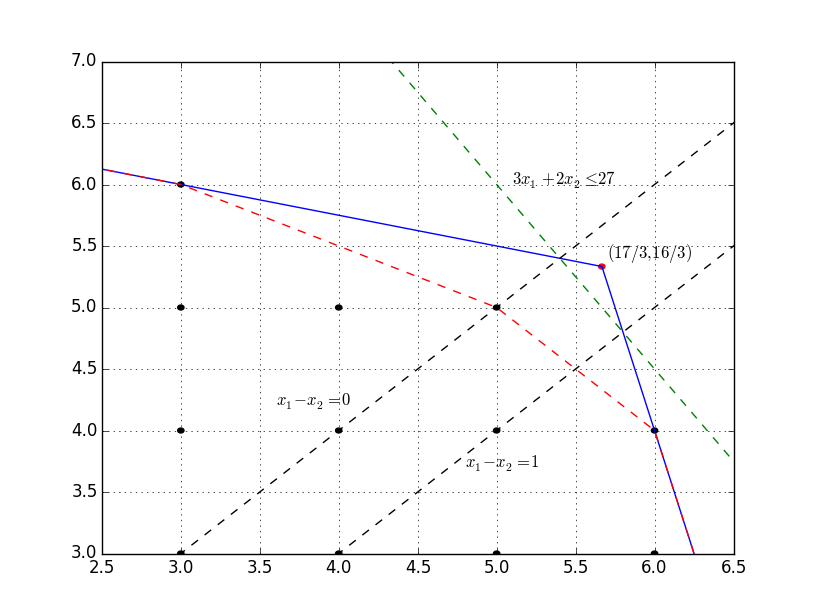
Figure 2 made with GrUMPy

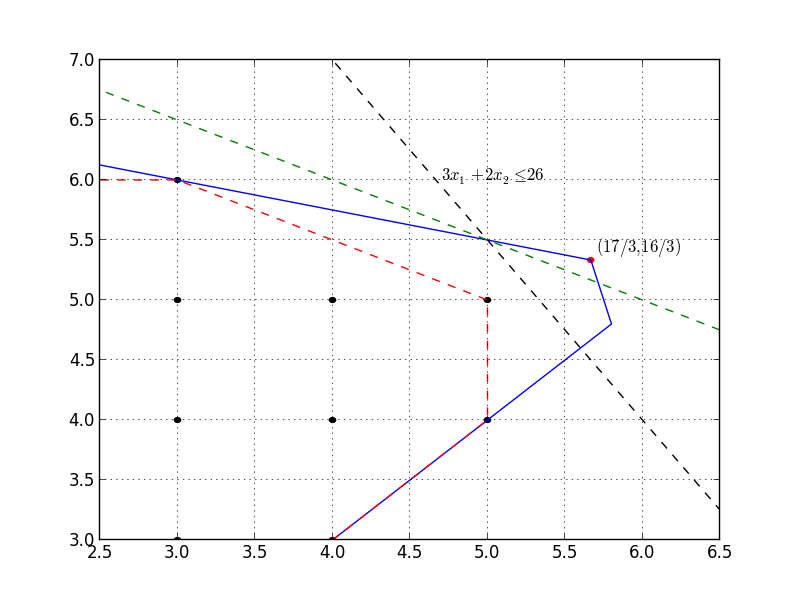
Figure 3 made with GrUMPy

Usage

Visualizing Branch and Bound Trees

There are two separate modes for visualizing branch and bound trees. One uses GiMPy to visualize the tree (which in turn uses GraphViz for layout). The other is to use the visualizations from the now-defunct Branch and Bound Analysis Kit (BAK), which was merged with GrUMPy. With the methods of the former BAK, one can visualize the tree in a number of ways using the venerated gnuplot (see a paper about it here).

The tree object itself can also be constructed in two different ways. The first is using the API of the BBTree class, as follows.

from coinor.grumpy import BBTree

T = BBTree()

#These can be any node attributes recognized by GraphViz
attr = {'color':'red',
        'style':'filled',
        'fillcolor':'red',
        'label':id}

T.AddOrUpdateNode(id = 0, parent_id = None,
                  branch_direction = None,
                  status = 'branched',
                  lp_bound = 100.2,
                  integer_infeasibility_count = 10,
                  integer_infeasibility_sum = 1.5,
                  condition_begin = None,
                  condition_end = None,
                  attr)

The properties of a node that are needed to visualize the tree with BAK are

The properties related to condition number are optional and utilized only if present. For visualizing the tree with GiMPy, only the id and parent_id are required (in the future, this may change).

The second way of constructing the tree is by parsing a log file from a solver. Any solver can be instrumented to generate a file that can then be used to visualize the tree and this can even be done "live" (subject to the speed at which the visualizations can be generated). The log file must contain one line for each event type. The events are primarily those that either create or change the status of nodes and in fact, the valid event types are exactly those listed above as valid node statuses with one addition: there is also an event called heuristic corresponding to the generation of a new solution found by a heuristic. The heuristic event is the only one that does not change the status of any node, just the global bound.

Each line of the log file consists of a space-separated list of fields. The fields are as follows:

  1. Time stamp.
  2. Event type (one of the statuses listed above or heuristic.
  3. The id of the node being created or changing status.
  4. The id of the node's parent.
  5. The branch direction (R or L).

The remaining fields differ by event type.

A snippet from an example file might look as follows (see, e.g., p0201_SYMPHONY.vbc):

  0.288516 branched 1 0 M 7125.000000 11.368421 24 19000000 100000
  0.289231 candidate 2 1 R 7465.000000
  0.289739 candidate 3 1 L 7125.000000
  0.302334 branched 3 1 L 7125.000000 11.368421 24 4750000 4750000
  0.302859 candidate 4 3 R 7125.000000
  0.303312 candidate 5 3 L 7125.000000
  0.311040 branched 4 3 R 7465.000000 7.500000 15 500000 500000
  0.311567 candidate 6 4 R 7465.000000
  0.312036 candidate 7 4 L 7465.000000
  0.317941 branched 6 4 R 7715.000000 6.250000 13 2000000000 2000000000
  0.318476 candidate 8 6 R 7715.000000
  0.318952 candidate 9 6 L 7715.000000
   .
   .
   .
 11.512976 integer 568 522 R 7805.000000
 11.513654 fathomed 1070 569 R
 11.514258 fathomed 1066 208 R
 11.514856 fathomed 1067 208 L
   .
   .
   .

The file can be processed as follows (see, e.g., BBVis.py:

from coinor.grumpy import BBTree

bt = BBTree()
file = open('vbc.out', 'r')
for line in file:
    bt.ProcessLine(line)

To display the visualizations, do

# BAK style
bt.set_display_mode('matplotlib')
bt.display('tree')

# Graphviz style
bt.set_layout('dot')
bt.display()

Visualizing Polyhedra

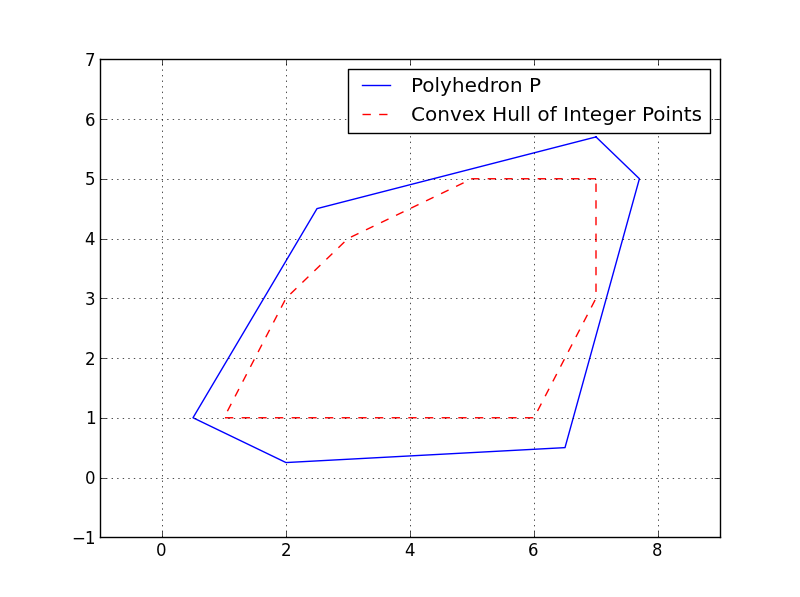
GrUMPy can be used to visualize polyhedra in two dimensions using the module polyhedron (see, e.g., DisplayPolyhedronAndSolveLP.py).

from coinor.grumpy.polyhedron2D import Polyhedron2D, Figure
points = [[2.5, 4.5], [6.5, 0.5], [0.5, 1],
          [7, 5.7], [7.7, 5], [2, 0.25]]
rays = []
c = [2, 5]
opt = [7, 5.7]
loc = (opt[0]+0.1, opt[1]-0.1)
obj_val = 42.5

p = Polyhedron2D(points = points, rays = rays)
f = Figure()
f.add_polyhedron(p, label = 'Polyhedron $P$', color = 'red')
f.set_xlim([p.xlim[0], p.xlim[1]+1])
f.set_ylim([p.ylim[0], p.ylim[1]+2])
f.add_line(c, obj_val, p.xlim + [0.2, 0.8], p.ylim + [0.2, 1.8], 
           linestyle = 'dashed', color = 'black', label = "Objective Function")
f.add_point(opt, 0.04, 'red')
f.add_text(loc, r'$x^* = %s$' % str(opt))
f.show()