Awesome

DynamicGrids is a generalised framework for building high-performance grid-based spatial simulations, including cellular automata, but also allowing a wider range of behaviours like random jumps and interactions between multiple grids. It is extended by Dispersal.jl for modelling organism dispersal processes.

DynamicGridsGtk.jl provides a simple live interface, while DynamicGridsInteract.jl also has live control over model parameters while the simulation runs: real-time visual feedback for manual parametrisation and model exploration.

DynamicGrids can run rules on single CPUs, threaded CPUs, and on CUDA GPUs. Simulation run-time is usually measured in fractions of a second.

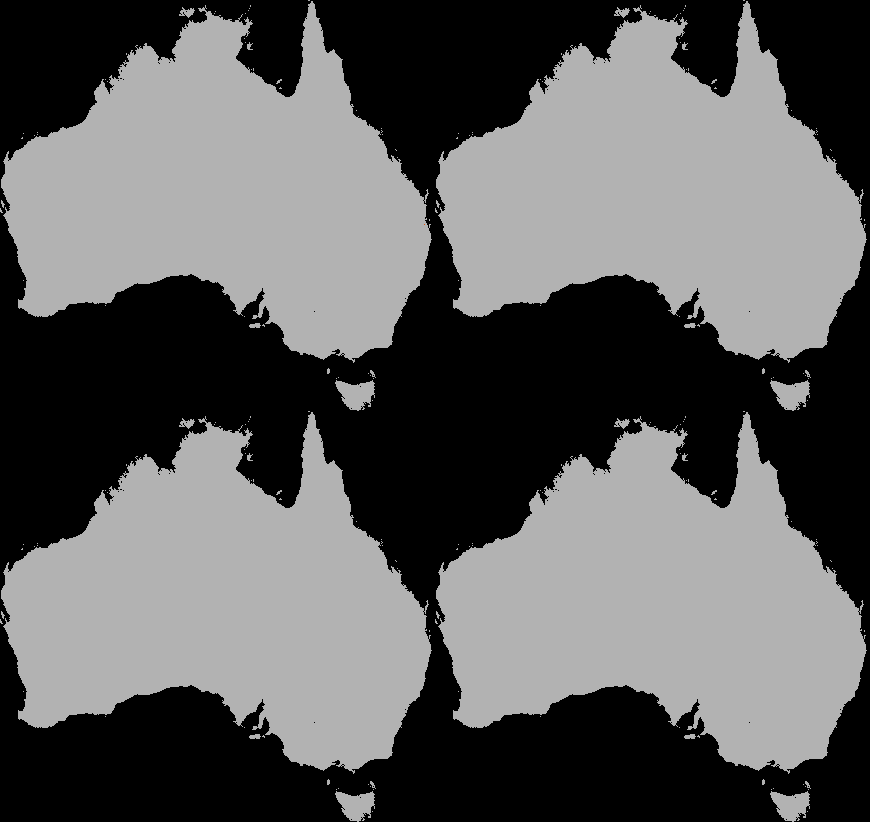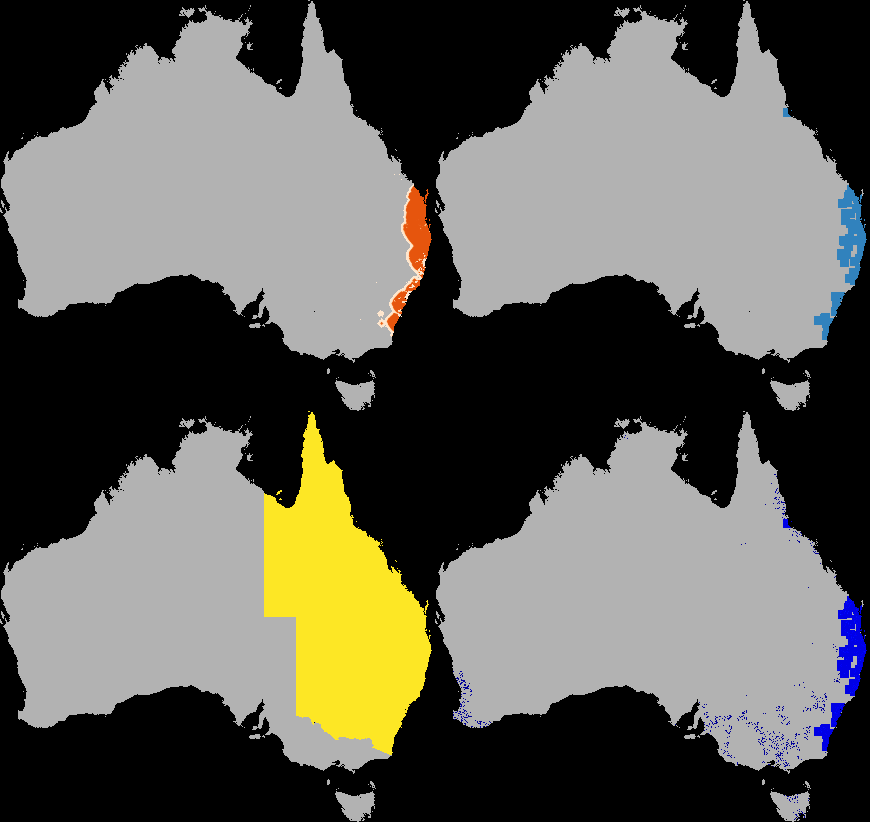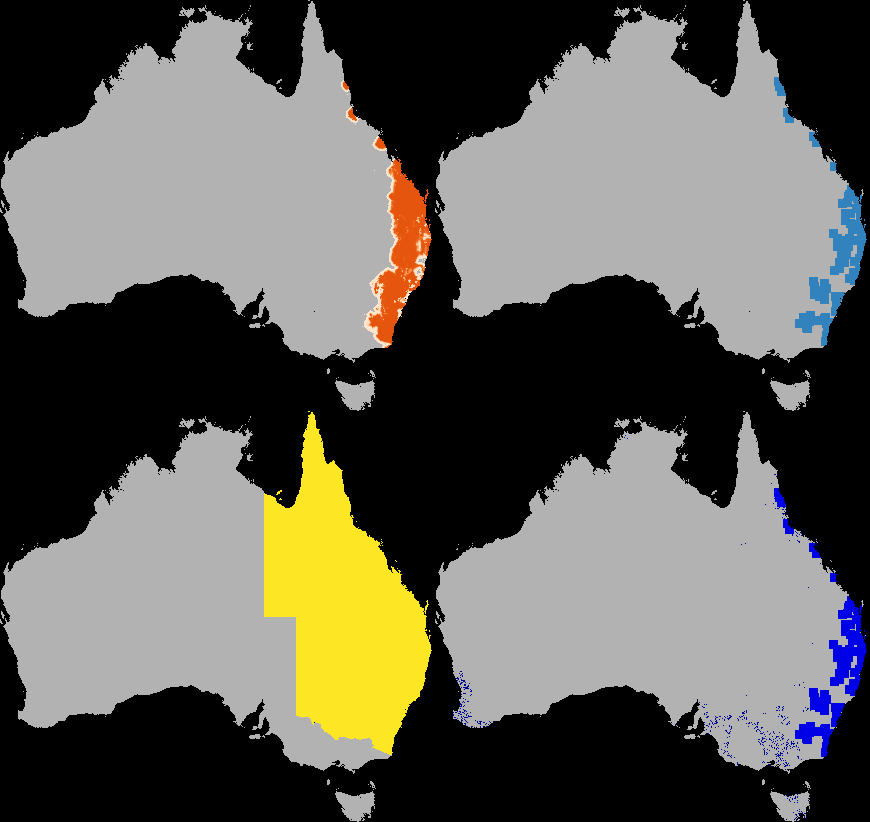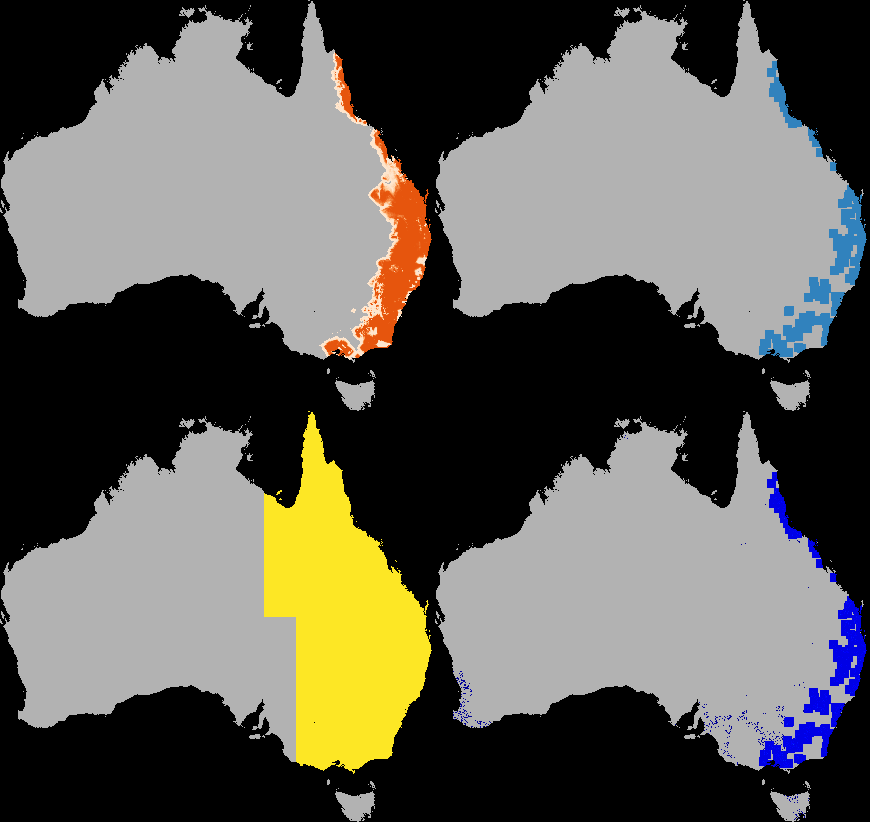
A dispersal simulation with quarantine interactions, using Dispersal.jl, custom rules and the GtkOuput from DynamicGridsGtk. Note that this is indicative of the real-time frame-rate on a laptop.

A DynamicGrids.jl simulation is run with a script like this one running the included game of life model Life():

using DynamicGrids, Crayons

init = rand(Bool, 150, 200)
output = REPLOutput(init; tspan=1:200, fps=30, color=Crayon(foreground=:red, background=:black, bold=true))
sim!(output, Life())

# Or define it from scratch (yes this is actually the whole implementation!)
life = Neighbors(Moore(1)) do data, hood, state, I
    born_survive = (false, false, false, true, false, false, false, false, false), 
                   (false, false, true, true,  false, false, false, false, false)
    born_survive[state + 1][sum(hood) + 1]
end
sim!(output, life)

A game of life simulation being displayed directly in a terminal.

Concepts

The framework is highly customisable, but there are some central ideas that define how a simulation works: grids, rules, and outputs.

Grids

Simulations run over one or many grids, derived from init of a single AbstractArray or a NamedTuple of multiple AbstractArray. Grids (GridData types) are, however not a single array but both source and destination arrays, to maintain independence between cell reads and writes where required. These may be padded or otherwise altered for specific performance optimisations. However, broadcasted getindex operations are guaranteed to work on them as if the grid is a regular array. This may be useful running simulations manually with step!.

Grid contents

Often grids contain simple values of some kind of Number, but other types are possible, such as SArray, FieldVector or other custom structs. Grids are updated by Rules that are run for every cell, at every timestep.

NOTE: Grids of mutable objects (e.g Array or any mutable struct have undefined behaviour. DynamicGrids.jl does not deepcopy grids between frames as it is expensive, so successive frames will contain the same objects. Mutable objects will not work at all on GPUs, and are relatively slow on CPUs. Instead, use regular immutable structs and StaticArrays.jl if you need arrays. Update them using @set from Setfield.jl or Accessors.jl, and generally use functional programming approaches over object-oriented ones.

Init

The init grid/s contain whatever initialisation data is required to start a simulation: the array type, size and element type, as well as providing the initial conditions:

init = rand(Float32, 100, 100)

An init grid can be attached to an Output:

output = ArrayOutput(init; tspan=1:100)

or passed in to sim!, where it will take preference over the init attached to the Output, but must be the same type and size:

sim!(output, ruleset; init=init)

For multiple grids, init is a NamedTuple of equal-sized arrays matching the names used in each Ruleset :

init = (predator=rand(100, 100), prey=(rand(100, 100))

Handling and passing of the correct grids to a Rule is automated by DynamicGrids.jl, as a no-cost abstraction. Rules specify which grids they require in what order using the first two (R and W) type parameters.

Dimensional or spatial init grids from DimensionalData.jl or GeoData.jl will propagate through the model to return output with explicit dimensions. This will plot correctly as a map using Plots.jl, to which shape files and observation points can be easily added.

Non-Number Grids

Grids containing custom and non-Number types are possible, with some caveats. They must define Base.zero for their element type, and should be a bitstype for performance. Tuple does not define zero. Array is not a bitstype, and does not define zero. SArray from StaticArrays.jl is both, and can be used as the contents of a grid. Custom structs that defne zero should also work.

However, for any multi-values grid element type, you will need to define a method of DynamicGrids.to_rgb that returns an ARGB32 for them to work in ImageOutputs, and isless for the REPLoutput to work. A definition for multiplication by a scalar Real and addition are required to use Convolution kernels.

Rules

Rules hold the parameters for running a simulation, and are applied in applyrule method that is called for each of the active cells in the grid. Rules come in a number of flavours (outlined in the docs). This allows using specialised methods for different types of rules, ecoding assumtions about their behaviours that can greatly improve performance through more efficient use of caches and parallelisation. Rules can be collected in a Ruleset, with some additional arguments to control the simulation:

ruleset = Ruleset(Life(2, 3); opt=SparseOpt(), proc=CuGPU())

Multiple rules can be combined in a Ruleset or simply passed to sim! directly. Each rule will be run for the whole grid, in sequence, using appropriate optimisations depending on the parent types of each rule:

ruleset = Ruleset(rule1, rule2; timestep=Day(1), opt=SparseOpt(), proc=ThreadedCPU())

Output

Outputs are ways of storing or viewing a simulation. They can be used interchangeably depending on your needs: ArrayOutput is a simple storage structure for high performance-simulations. As with most outputs, it is initialised with the init array, but in this case it also requires the number of simulation frames to preallocate before the simulation runs.

output = ArrayOutput(init; tspan=1:10)

The REPLOutput shown above is a GraphicOutput that can be useful for checking a simulation when working in a terminal or over ssh:

output = REPLOutput(init; tspan=1:100)

ImageOutput is the most complex class of outputs, allowing full color visual simulations using ColorSchemes.jl. It can also display multiple grids using color composites or layouts, as shown above in the quarantine simulation.

DynamicGridsInteract.jl provides simulation interfaces for use in Juno, Jupyter, web pages or electron apps, with live interactive control over parameters, using ModelParameters.jl. DynamicGridsGtk.jl is a simple graphical output for Gtk. These packages are kept separate to avoid dependencies when being used in non-graphical simulations.

Outputs are also easy to write, and high performance applications may benefit from writing a custom output to reduce memory use, or using TransformedOuput. Performance of DynamicGrids.jl is dominated by cache interactions, so reducing memory use has positive effects.

Example: Forest Fire

This example implements the classic stochastic forest fire model in a few different ways, and benchmarks them. Note you will need ImageMagick.jl installed for .gif output to work.

First we will define a Forest Fire algorithm that sets the current cell to burning, if a neighbor is burning. Dead cells can come back to life, and living cells can spontaneously catch fire:

using DynamicGrids, ColorSchemes, Colors, BenchmarkTools

const DEAD, ALIVE, BURNING = 1, 2, 3

neighbors_rule = let prob_combustion=0.0001, prob_regrowth=0.01
    Neighbors(Moore(1)) do data, neighborhood, cell, I
        if cell == ALIVE
            if BURNING in neighborhood
                BURNING
            else
                rand() <= prob_combustion ? BURNING : ALIVE
            end
        elseif cell == BURNING
            DEAD
        else
            rand() <= prob_regrowth ? ALIVE : DEAD
        end
    end
end

# Set up the init array and output (using a Gtk window)
init = fill(ALIVE, 400, 400)
output = GifOutput(init; 
    filename="forestfire.gif", 
    tspan=1:200, 
    fps=25, 
    minval=DEAD, maxval=BURNING, 
    scheme=ColorSchemes.rainbow,
    zerocolor=RGB24(0.0)
)

# Run the simulation, which will save a gif when it completes
sim!(output, neighbors_rule)

Timing the simulation for 200 steps, the performance is quite good. This particular CPU has six cores, and we get a 5.25x speedup by using all of them, which indicates good scaling:

bench_output = ResultOutput(init; tspan=1:200)

julia> 
@btime sim!($bench_output, $neighbors_rule);
  477.183 ms (903 allocations: 2.57 MiB)

julia> @btime sim!($bench_output, $neighbors_rule; proc=ThreadedCPU());
  91.321 ms (15188 allocations: 4.07 MiB)

We can also invert the algorithm, setting cells in the neighborhood to burning if the current cell is burning, by using the SetNeighbors rule:

setneighbors_rule = let prob_combustion=0.0001, prob_regrowth=0.01
    SetNeighbors(Moore(1)) do data, neighborhood, cell, I
        if cell == DEAD
            if rand() <= prob_regrowth
                data[I...] = ALIVE
            end
        elseif cell == BURNING
            for pos in positions(neighborhood, I)
                if data[pos...] == ALIVE
                    data[pos...] = BURNING
                end
            end
            data[I...] = DEAD
        elseif cell == ALIVE
            if rand() <= prob_combustion 
                data[I...] = BURNING
            end
        end
    end
end

Note: we are not using add!, instead we just set the grid value directly. This usually risks errors if multiple cells set different values. Here they only ever set a currently living cell to burning in the next timestep. It doesn't matter if this happens multiple times, the result is the same.

And in this case (a fairly sparse simulation), this rule is faster:

julia> @btime sim!($bench_output, $setneighbors_rule);
  261.969 ms (903 allocations: 2.57 MiB)

julia> @btime sim!($bench_output, $setneighbors_rule; proc=ThreadedCPU());
  65.489 ms (7154 allocations: 3.17 MiB)

But the scaling is not quite as good, at 3.9x for 6 cores. The first method may be better on a machine with a lot of cores.

Last, we slightly rewrite these rules for GPU, as rand was not available within a GPU kernel. It is now, but it turns out that this method is faster! and interesting to demonstrate using multiple grids and SetGrid.

This way we call CUDA.rand! on the entire parent array of the :rand grid, using a SetGrid rule:

using CUDAKernels, CUDA

randomiser = SetGrid{Tuple{},:rand}() do randgrid
    CUDA.rand!(parent(randgrid))
end

Now we define a Neighbors version for GPU, using the :rand grid values instead of rand():

neighbors_gpu = let prob_combustion=0.0001, prob_regrowth=0.01
    Neighbors{Tuple{:ff,:rand},:ff}(Moore(1)) do data, neighborhood, (cell, rand), I
        if cell == ALIVE
            if BURNING in neighborhood
                BURNING
            else
                rand <= prob_combustion ? BURNING : ALIVE
            end
        elseif cell == BURNING
            DEAD
        else
            rand <= prob_regrowth ? ALIVE : DEAD
        end
    end
end

And a SetNeighbors version for GPU:

setneighbors_gpu = let prob_combustion=0.0001, prob_regrowth=0.01
    SetNeighbors{Tuple{:ff,:rand},:ff}(Moore(1)) do data, neighborhood, (cell, rand), I
        if cell == DEAD
            if rand <= prob_regrowth
                data[:ff][I...] = ALIVE
            end
        elseif cell == BURNING
            for pos in positions(neighborhood, I)
                if data[:ff][pos...] == ALIVE
                    data[:ff][pos...] = BURNING
                end
            end
            data[:ff][I...] = DEAD
        elseif cell == ALIVE
            if rand <= prob_combustion 
                data[:ff][I...] = BURNING
            end
        end
    end
end

Now benchmark both version on a GTX 1080 GPU. Despite the overhead of reading and writing two grids, this turns out to be even faster again:

bench_output_rand = ResultOutput((ff=init, rand=zeros(size(init))); tspan=1:200)

julia> @btime sim!($bench_output_rand, $randomiser, $neighbors_gpu; proc=CuGPU());
  30.621 ms (186284 allocations: 17.19 MiB)

julia> @btime sim!($bench_output_rand, $randomiser, $setneighbors_gpu; proc=CuGPU());
  22.685 ms (147339 allocations: 15.61 MiB)

That is, we are running the rule at a rate of 1.4 billion times per second. These timings could be improved (maybe 10-20%) by using grids of Int32 or Int16 to use less memory and cache. But we will stop here.