Awesome

gomath

Extra mathematical algorithms and data types for Golang.

Packages

The repository provides the following packages:

Follow the godoc links above to find more about each package.

Quick overview

Let's consider a few examples for each package here.

rational

The package provides the Rational data type and a kit of corresponding methods to work with rational numbers.

Imagine you have the following expression to solve:

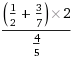
example 1

Here's how to solve it using the rational package:

package main

import (
	"log"

	"github.com/alex-ant/gomath/rational"
)

func main() {
	// Create a new rational number defining it's numerator and denominator.
	r1 := rational.New(1, 2)
	// This also can be done using an existing float number.
	r1, err := rational.NewFromFloat(0.5)
	if err != nil {
		log.Fatal(err)
	}

	r2 := rational.New(3, 7)
	r3 := rational.New(4, 5)

	// Add 3/7 to 1/2, multiply by 2 and divide by 4/5.
	result := r1.Add(r2).MultiplyByNum(2).Divide(r3)
	log.Println(result)           // {65 28}
	log.Println(result.Float64()) // 2.3214285714285716
}

gaussian

The package solves systems of linear equations via the Gaussian Elimination method. It also can solve the system in case one or more variables remain unknown printing the corresponding relations.

An example system where all the variables meant to be found (x1 = 1, x2 = 2, x3 = 3, x4 = 4):

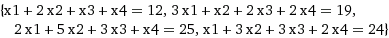
example 2

Here's how to solve it using the gaussian package:

package main

import (
	"log"

	"github.com/alex-ant/gomath/gaussian-elimination"
	"github.com/alex-ant/gomath/rational"
)

func main() {
	nr := func(i int64) rational.Rational {
		return rational.New(i, 1)
	}

	equations := make([][]rational.Rational, 4)
	equations[0] = []rational.Rational{nr(1), nr(2), nr(1), nr(1), nr(12)}
	equations[1] = []rational.Rational{nr(3), nr(1), nr(2), nr(2), nr(19)}
	equations[2] = []rational.Rational{nr(2), nr(5), nr(3), nr(1), nr(25)}
	equations[3] = []rational.Rational{nr(1), nr(3), nr(3), nr(2), nr(24)}

	res, gausErr := gaussian.SolveGaussian(equations, false)
	if gausErr != nil {
		log.Fatal(gausErr)
	}

	for _, v := range res {
		log.Println(v)
	}
	// Output:
	// [{1 1}]
	// [{2 1}]
	// [{3 1}]
	// [{4 1}]
}

If we remove the 4th equation from the system, the solver won't be able to determine all the variables, although it will tell exactly which variable can take any value and how others depend on it:

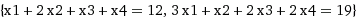
example 3

Solving the system the same way:

package main

import (
	"log"

	"github.com/alex-ant/gomath/gaussian-elimination"
	"github.com/alex-ant/gomath/rational"
)

func main() {
	nr := func(i int64) rational.Rational {
		return rational.New(i, 1)
	}

	equations := make([][]rational.Rational, 2)
	equations[0] = []rational.Rational{nr(1), nr(2), nr(1), nr(1), nr(12)}
	equations[1] = []rational.Rational{nr(3), nr(1), nr(2), nr(2), nr(19)}

	res, gausErr := gaussian.SolveGaussian(equations, false)
	if gausErr != nil {
		log.Fatal(gausErr)
	}

	for _, v := range res {
		log.Println(v)
	}
	// Output:
	// [{26 5} {3 5} {3 5}]
	// [{17 5} {1 5} {1 5}]
	// [{0 0}]
	// [{0 0}]
}

The output means that x3 and x4 can take any value and x1 and x2 depend on them the following way:

example 4