Home

Awesome

UGM

Ubpa Graphics Mathematics，Ubpa 图形数学库

⭐ Star us on GitHub — it helps!

repo-size tag license

特点

1. 简介

UGM 是着重于代数概念的数学库，区分点、向量、法向、颜色等，从而尽可能地避免了错误的计算。

常用的图形数学库（如 Eigen，glm）只提供 vec 类，并使其能做各种运算（如 +-*/ 等），但从代数方面考虑，这并不合理。

示例

我们通过提供 point，vec，normal，rgb 等来区分不同的代数概念，并仅让他们支持合理的操作，这样就能在编译期就发现各种代数方面的错误，另外还能减轻心智负担（根据类型执行不同的操作）。

此外，我们还通过单继承的技术实现了极佳的代码编写，特点如下

2. 示例

#include <UGM/UGM.h>

using namespace Ubpa;
using namespace std;

int main() {
    transformf tsfm{
        vecf3{1,1,1},                        // T
        quatf{vecf3{1,0,0}, to_radian(90.f), // R
        scalef3{2.f}}                        // S
    }; // T * R * S

    pointf3 p{ 1,2,3 };
    vecf3 v{ 1,1,1 };
    normalf n{ 0,1,0 };
    bboxf3 b{ p, p + v }; // min: 1 2 3, max: 2 3 4
    rayf3 r{ p, v }; // point: 1 2 3, dir: 1 1 1, tmin: EPSILON, tmax: FLT_MAX

    cout << tsfm * p << endl; // 3 -5 5
    cout << tsfm * v << endl; // 2 -2 2
    cout << tsfm * n << endl; // 0 0 0.5
    cout << tsfm * b << endl; // 3 -7 5, 5 -5 7
    cout << tsfm * r << endl; // 3 -5 5, 2 -2 2, EPSILON, FLT_MAX

    return 0;
}

3. 文档

4. 设计思路

为了更好地使用该数学库，我们很有必要先了解下该库的设计思路。

4.1 代数概念

该库着重于正确的代数概念，使用者很可能对这方面并不了解，但只要知道基础的线性代数知识即可。

下边我简单介绍下该库涉及的主要代数概念。

4.2 底层存储类型

由于底层存储类型不同，上述代数概念的具体实现有所不同（抽象 => 具体），并引申出新的代数概念

4.2.1 数组

底层存储类型为数组时，则可引申出如下代数概念

上述各种概念在具体为数组时会有对应的实现，如

T operator+(T a, T b) const {
    return {a[0]+b[0], a[1]+b[1], a[2]+b[2]};
}

4.2.2 矩阵

由于该库用于离线渲染，实时渲染，游戏等，基本只要用 float4，因此也只需 3x3 和 4x4 的矩阵，因此该库也限制为只支持 3x3 和 4x4 的矩阵(并特化矩阵的乘法与逆的实现，如循环展开，simd 加速，以提高性能)。

大型矩阵的支持一般需要用线性代数库，如 Eigen 等。

底层通过一维数组的数组来实现，右乘，列优先，同于 OpenGL 与 DX（右乘+列优先的方案十分适合于 SIMD，同理左乘+行优先也如此）。

4.3 类

通过组合多个代数概念并加上具体类型支持的操作，可以轻松得到各种各样的代数类。他们满足不同的操作，极大地帮助使用者避免错误。

目前各种组合（主要部分）如下

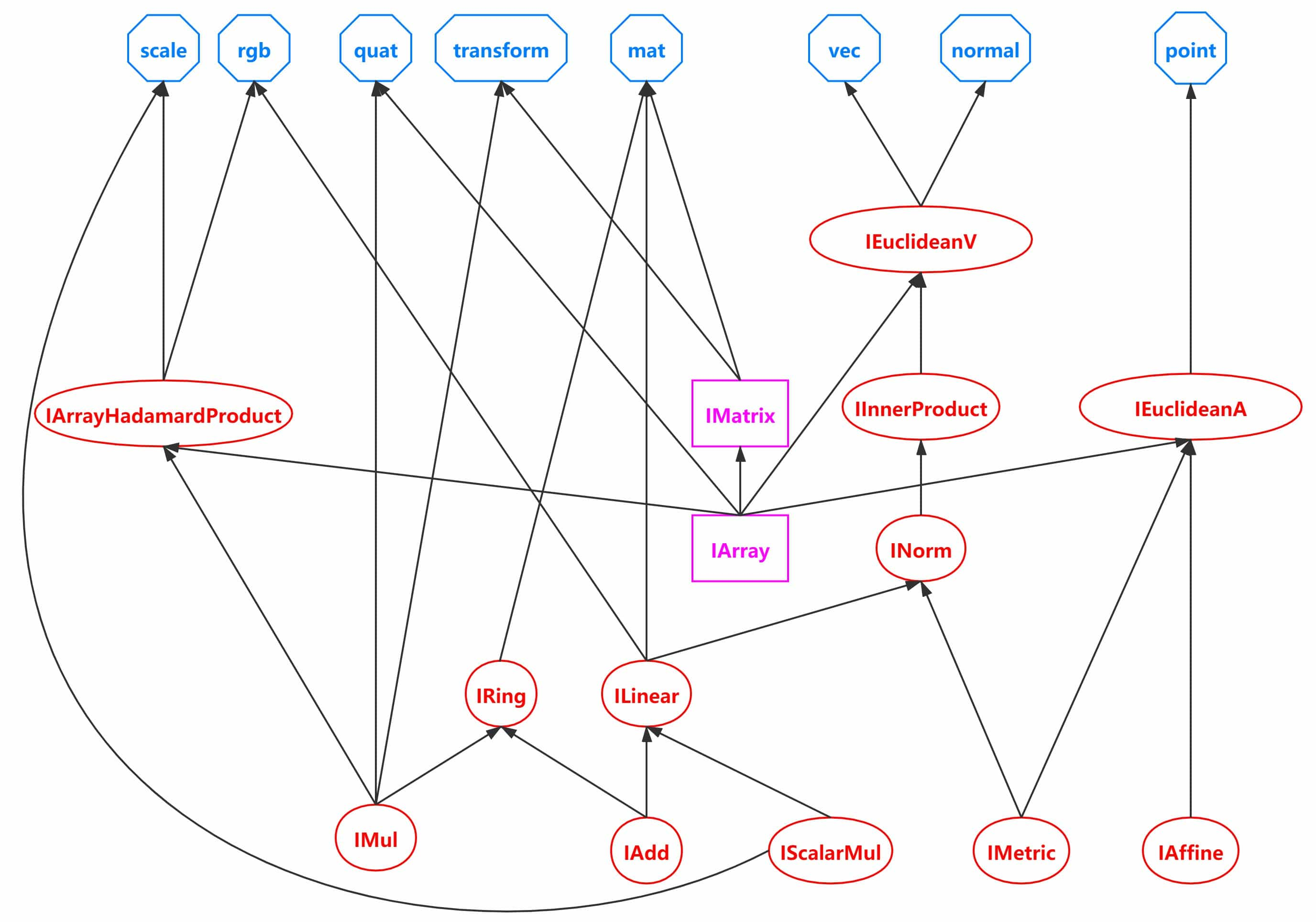
graph.jpg

若图片加载失败，请用该链接 graph.jpg

图中含有的类有

该库还含有类

5. 接口

类由多个代数概念组合而成，所以关键在于把握代数概念的接口，各代数概念位于 include/UGM/Interfaces/。

所有接口都是类方法，方便使用，大部分情况下都可以利用 IDE 的代码提示功能（如 VS2019 的 intellisense）来查询接口。

此外还提供了渲染领域常见函数 / 算法，如相交（位于 line，ray 内）、采样、材质 等。

6. SIMD

该库支持 SIMD，只要求支持 SSE2 指令。

主要加速的类为 float4，包括 vecf4，pointf4 等。

注意 float3 并没有 SIMD 加速，这是为了保持 sizeof(float3)==3*sizeof(float)，部分数学库通过使用含 __m128 的 float3 来实现 SIMD 加速，但这样 sizeof(float3)==4*sizeof(float)。目前可以通过显式将 float3 转成 float4 来获取加速效果。

加速部分包括

7. Natvis

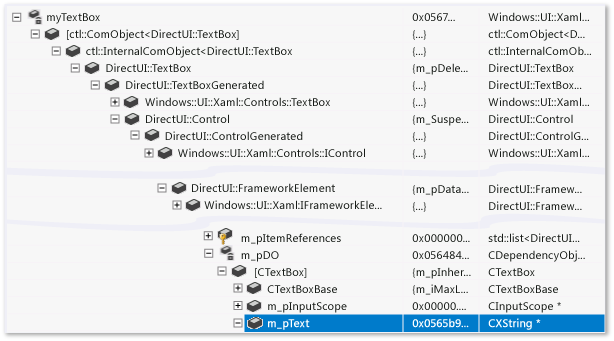
泛型编程在 debug 时会引入大量的单继承，该库使用了单继承化技术，单继承深度也很大，导致在 IDE 中查看类成员变量会很麻烦。

示例

TextBox default visualization

若图片加载失败，请用该链接 TextBox default visualization

我们可使用 VS2019 的 natvis 功能来实现定制的视图

natvis_demo.jpg

若图片加载失败，请用该链接 natvis_demo.jpg

当使用 find_package(UGM REQUIRED) 时，会自动给解决方案添加一个项目，包含 UGM_<VERSION>.natvis，从而使得其他项目都可以支持 natvis（VS2019 支持多种方式引入 natvis，但这是目前我能想到的最合适的方式）。

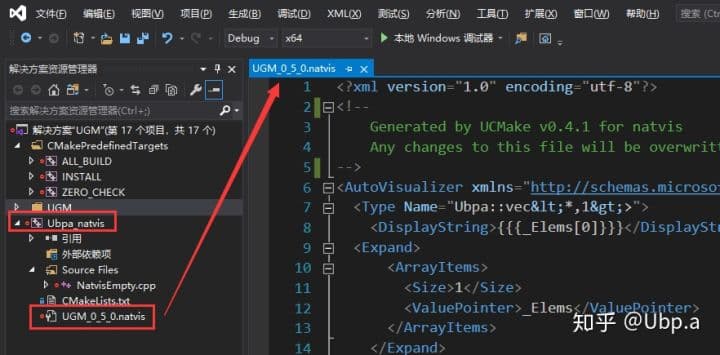
use_natvis.jpg

若图片加载失败，请用该链接 use_natvis.jpg

Future Features

Copyright and Licensing

You can copy and paste the license summary from below.

MIT License

Copyright (c) 2020 Ubpa

Permission is hereby granted, free of charge, to any person obtaining a copy
of this software and associated documentation files (the "Software"), to deal
in the Software without restriction, including without limitation the rights
to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
copies of the Software, and to permit persons to whom the Software is
furnished to do so, subject to the following conditions:

The above copyright notice and this permission notice shall be included in all
copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
SOFTWARE.