Awesome

Spatio-Temporal-Graph-Convolutional-Networks-A-Deep-Learning-Framework-for-Traffic-Forecasting

linear regression perform well on short interval forecast instead of long terms
this is a data-driven and using spotio-temporal information method.
fully utilize spatio-information instead of treating it as discrete units
$$\hat v_{t+1},...,\hat v_{t+H} = argmax log_{10} P(v_{t+1},...,v_{t+H}|v_{t-M},...,v_{t})$$
where $$v_t \in R^n$$, n is an observation vector of n road segments at time step t

convolution on graphs

normalized Laplacian
- Random walk normalized Laplacian
- analogy to The Multivariate Gaussian Distribution
- Symmetric normalized Laplacian L: $laplacian$
first generation of GNC $y_{output}=\sigma \left(U\left(\begin{matrix}\theta_1 &\\&\ddots \\ &&\theta_n \end{matrix}\right) U^T x \right) \qquad(3)$
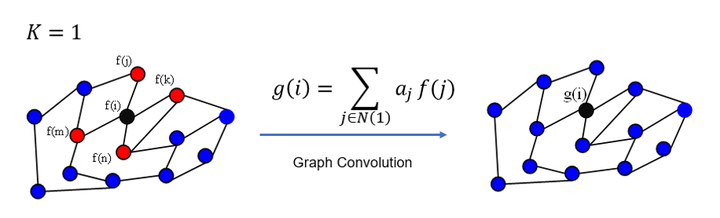
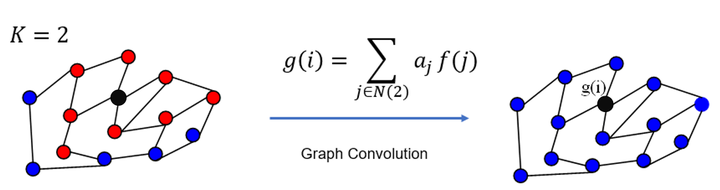
second generation of GNC $y_{output}=\sigma \left(U\left(\begin{matrix}\sum_{j=0}^K \alpha_j \lambda^j_1 &\\&\ddots \\ && \sum_{j=0}^K \alpha_j \lambda^j_n \end{matrix}\right) U^T x \right) \qquad(4)$ $U \sum_{j=0}^K \alpha_j \Lambda^j U^T =\sum_{j=0}^K \alpha_j U\Lambda^j U^T = \sum_{j=0}^K \alpha_j L^j$ $y_{output}=\sigma \left( \sum_{j=0}^K \alpha_j L^j x \right) \qquad(5)$
- if k == n, receptive field is n hop
third generation of GNC
- where $$c_1$$, $$c_2$$ and $$c_3$$ are fixed
- The only trainable parameters are $$\theta_0$$ and $$\theta_1$$
- in the final version the authors even further fix $$\theta_0 = -\theta_1$$