Awesome

A Tensorflow Implementation of "Riemannian approach to batch normalization"

This code was used for experiments in Riemannian approach to batch normalization (NIPS 2017) by Minhyung Cho and Jaehyung Lee (https://arxiv.org/abs/1709.09603). The poster for the conference can be found here.

Refer to https://github.com/MinhyungCho/riemannian-batch-normalization-pytorch for a PyTorch implementation.

Abstract

Batch Normalization (BN) has proven to be an effective algorithm for deep neural network training by normalizing the input to each neuron and reducing the internal covariate shift. The space of weight vectors in the BN layer can be naturally interpreted as a Riemannian manifold, which is invariant to linear scaling of weights. Following the intrinsic geometry of this manifold provides a new learning rule that is more efficient and easier to analyze. We also propose intuitive and effective gradient clipping and regularization methods for the proposed algorithm by utilizing the geometry of the manifold. The resulting algorithm consistently outperforms the original BN on various types of network architectures and datasets.

Results

Classifiation error rate on CIFAR (median of five runs):

Classification error rate on SVHN (median of five runs):

WRN-28-10 on CIFAR10	WRN-28-10 on CIFAR100	WRN-22-8 on SVHN

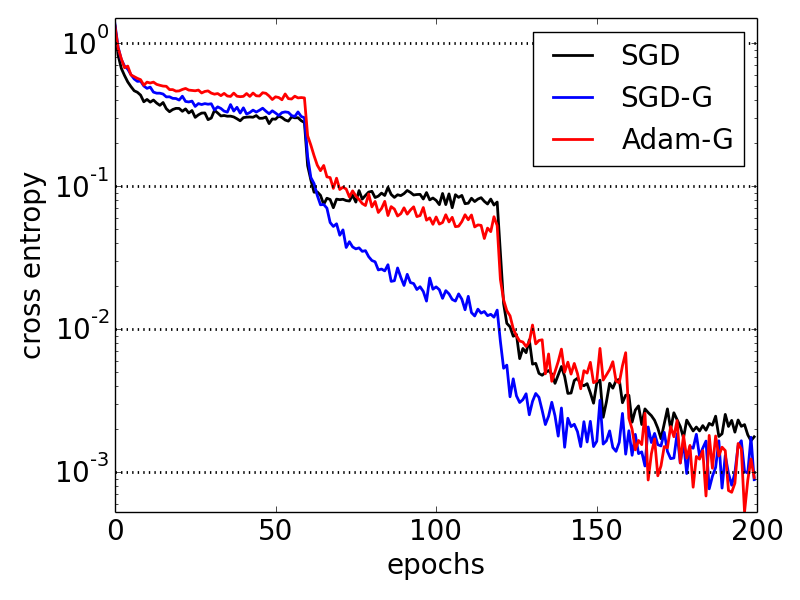See https://arxiv.org/abs/1709.09603 for details.

Dependencies

• Python 3
• NumPy
• SciPy (for SVHN experiments)
• Tensorflow >= 1.2

Train

The commands below are examples for reproducing results in the paper.

CIFAR10:

[SGD] python3 train.py --model=resnet --depth=28 --widen_factor=10 --optimizer=sgd --learnRate=0.1 --weightDecay=0.0005 --biasDecay=0.0005 --gammaDecay=0.0005 --betaDecay=0.0005 --keep_prob=0.7 --data=cifar10
[SGD-G] python3 train.py --model=resnet --depth=28 --widen_factor=10 --optimizer=sgdg --grassmann=True --learnRate=0.01 --learnRateG=0.2 --omega=0.1 --grad_clip=0.1 --weightDecay=0.0005 --keep_prob=0.7 --data=cifar10
[Adam-G] python3 train.py --model=resnet --depth=28 --widen_factor=10 --optimizer=adamg --grassmann=True --learnRate=0.01 --learnRateG=0.05 --omega=0.1 --grad_clip=0.1 --weightDecay=0.0005 --keep_prob=0.7 --data=cifar10

CIFAR100:

[SGD] python3 train.py --model=resnet --depth=28 --widen_factor=10 --optimizer=sgd --learnRate=0.1 --weightDecay=0.0005 --biasDecay=0.0005 --gammaDecay=0.0005 --betaDecay=0.0005 --keep_prob=0.7 --data=cifar100
[SGD-G] python3 train.py --model=resnet --depth=28 --widen_factor=10 --optimizer=sgdg --grassmann=True --learnRate=0.01 --learnRateG=0.2 --omega=0.1 --grad_clip=0.1 --weightDecay=0.0005 --keep_prob=0.7 --data=cifar100
[Adam-G] python3 train.py --model=resnet --depth=28 --widen_factor=10 --optimizer=adamg --grassmann=True --learnRate=0.01 --learnRateG=0.05 --omega=0.1 --grad_clip=0.1 --weightDecay=0.0005 --keep_prob=0.7 --data=cifar100

SVHN:

[SGD] python3 train.py --model=resnet --depth=22 --widen_factor=8 --optimizer=sgd --learnRate=0.01 --weightDecay=0.0005 --biasDecay=0.0005 --gammaDecay=0.0005 --betaDecay=0.0005 --keep_prob=0.6 --learnRateDecay=0.1 --data=svhn
[SGD-G] python3 train.py --model=resnet --depth=22 --widen_factor=8 --optimizer=sgdg --grassmann=True --learnRate=0.001 --learnRateG=0.02 --omega=0.1 --grad_clip=0.1 --weightDecay=0.0005 --keep_prob=0.6 --learnRateDecay=0.1 --data=svhn
[Adam-G] python3 train.py --model=resnet --depth=22 --widen_factor=8 --optimizer=adamg --grassmann=True --learnRate=0.001 --learnRateG=0.005 --omega=0.1 --grad_clip=0.1 --weightDecay=0.0005 --keep_prob=0.6 --learnRateDecay=0.1 --data=svhn

Another example:

[2GPUs] pyhon3 train.py --model=resnet --depth=40 --widen_factor=10 --optimizer=adamg --grassmann=True --learnRate=0.01 --learnRateG=0.05 --omega=0.1 --grad_clip=0.1 --weightDecay=0.0005 --keep_prob=0.7 --data=cifar100 --vali_batch_size=200 --num_gpus=2
[VGG-19] python3 train.py --model=vgg19 --optimizer=adamg --grassmann=True --learnRate=0.01 --learnRateG=0.05 --omega=0.1 --grad_clip=0.1 --weightDecay=0.0005 --data=cifar100

Test the performance of a checkpoint

python3 train.py --model=resnet --depth=40 --widen_factor=10  --data=cifar100 --task=test --load=./logs/resnet_train_cifar100/model.ckpt-78124

To apply this algorithm to your model

grassmann_optimizer.py is the main implementation which provides the proposed SGD-G and Adam-G optimizer, as well as HybridOptimizer, an abstract convenience class. train.py includes all the steps to apply the provided optimizers to your model.

1. Collect all the weight parameters which need to be optimized on Grassmann manifold (and initialize them to a unit scale):

   weight = [i for i in tf.trainable_variables() if 'weight' in i.name]
   undercomplete = np.prod(var.shape[0:-1])>var.shape[-1]
   if undercomplete and ('conv' in var.name):
       ## initialize to scale 1
       var._initializer_op=tf.assign(var, gutils.unit_initializer()(var.shape)).op
       tf.add_to_collection('grassmann', var)
   

2. Build the graph for orthogonality regularizer:

   for var in tf.get_collection('grassmann'):
       shape = var.get_shape().as_list()
       v = tf.reshape(var, [-1, shape[-1]])
       v_sim = tf.matmul(tf.transpose(v), v)
   
       eye = tf.eye(shape[-1])
       assert eye.get_shape()==v_sim.get_shape()
   
       orthogonality = tf.multiply(tf.reduce_sum( (v_sim-eye)**2 ), 0.5*FLAGS.omega, name='orthogonality')
       tf.add_to_collection('orthogonality', orthogonality)
   

   Do not apply weight decay to the parameters above.

3. Add orthogonality loss to the loss function:

   orthogonality = tf.add_n(tf.get_collection('orthogonality', scope), name='orthogonality')
   total_loss = cross_entropy_mean + weightcost + orthogonality
   

4. Initialze the optimizer:

   import grassmann_optimizer
   opta = tf.train.MomentumOptimizer(learning_rate, momentum)
   optb = grassmann_optimizer.SgdgOptimizer(learning_rate, momentum, grad_clip) # or use Adam-G
   opt = grassmann_optimizer.HybridOptimizer(opta, optb)
   

5. Build the training graph:

   Pass two lists of (gradient, variable) pairs to apply_gradients(). Variables in grads_a will be updated by opta and variables in grads_b will be updated by optb.

   grads_a = [i for i in grads if not i[1] in tf.get_collection('grassmann')]
   grads_b = [i for i in grads if i[1] in tf.get_collection('grassmann')]
   apply_gradient_op = opt.apply_gradients(grads_a, grads_b)