Home

Awesome

Anomalous Mackey-Glass Time Series

The Mackey-Glass Anomaly Benchmark

This repository contains the Mackey-Glass anomaly benchmark (MGAB), which is composed of synthetic Mackey-Glass time series with non-trivial anomalies. Mackey-Glass time series are known to exhibit chaotic behavior under certain conditions. MGAB contains 10 MG time series of length 10<sup>5</sup>. Into each time series 10 anomalies are inserted with a procedure as described below. In contrast to other synthetic benchmarks, it is very hard for the human eye to distinguish the introduced anomalies from the normal (chaotic) behavior. An excerpt of a time series containing 3 anomalies is shown in the graph above. The location of the anomalies are revealed in the last plot of this page.

Authors/Contributors

Citing this Repository

This repository can be cited using the following identifier: DOI

The benchmark is also used in the following paper: Thill, M., Konen, W., & Bäck, T. (2020, November). Time series encodings with temporal convolutional networks. In International Conference on Bioinspired Methods and Their Applications (pp. 161-173). Springer, Cham.

If you use the MGAB for your work as well, just let us know and we can add a reference to your publication here.

Download

The easiest way to download this repository is to clone it with Git: git clone https://github.com/MarkusThill/MGAB.git

The Benchmark Files

The labeled data for the time series 1-10 can be found in the CSV files [1-10].csv. Each file contains a table with 4 columns:

  1. time: Time in seconds in the range 0 to 10<sup>5</sup> -1.
  2. value: Value of x(t) in the range [0.26, 1.66].
  3. is_anomaly: Binary values (0/1) indicate which data points are considered as normal (0) or anomalous (1). For each anomaly, a range of 400 points, the so called anomaly window, is flagged. Detections within the anomaly window are to be considered as correct.
  4. is_ignored: Since some algorithms might require a "warm-up" phase when processing the time series, the is_ignored column indicates for the initial 256 time steps that false detections can be ignored. It was ensured that no anomalies were placed at the beginning of any time series.

Time Series Generation

We use the following Mackey-Glass equation (a non-linear time delay differential equation, DDE) to generate our time series:

\frac{dx}{dt} = \beta \cdot \frac{x(t-\tau)}{1+x(t-\tau)^n} - \gamma x(t)

The parameters are real numbers which we set to τ=18, n=10, β=0.25, γ=0.1. Additionally, a constant history parameter is required which is set to h=0.9. A sufficiently long time series is generated using the JiTCDDE solver ( with an integration stepsize of one) which is then divided into 10 new time series. The time delay embedding of such a time series is illustrated in Fig. 1.

Pseudo-code of the anomaly insertion procedure for Mackey-Glass time series.<br>Figure 1: Time delay embedding of the Mackey-Glass attractor.

Anomaly Insertion Process

The main idea of the anomaly insertion process is to randomly remove segments from each time series in a way that this will be hardly visible later. To do so, we try to find two points (with a minimal and maximal distance) in a random segment of the time series so that the values of these two points as well as their derivatives closely match. Then, we remove the segment between those two points and "stich" the remaining parts together again. The exact procedure is as follows:

  1. For the time series sequence x(t) estimate the first 3 derivatives dx/dt, d^2x/dx^2 and d^3x/dx^3 by numerical differentiation of x(t). Then, stack the original time series x(t) and the three derivatives in a four-dimensional time series \mathbf x(t).
  2. Randomly select a position t_i in \mathbf x(t). This will be the first split point
  3. Starting at t_i'=t_i+m, with m=100, for all k\in K$, $K={0,1,\ldots,100}, compare \mathbf x(t) to \mathbf x(t_i'+k) and compute the euclidean norm d(k)=||\mathbf x(t_i) - \mathbf x(t_i'+k)||.
  4. The index k which minimizes the distance d(k) will give us the second split point t_j=t_i'+k_m, where k_m=\argmin_{k\in K} d(k)
  5. Construct a new manipulated time series x_m(t), which is x(t), for t\le t_i and x(t+m+k_m) for t > t_i.

The procedure is also summarized in Algorithm 1 below. Pseudo-code of the anomaly insertion procedure for Mackey-Glass time series.

An example of how such an anomaly, which was generated using the described procedure, could look like is illustrated in Fig. 2. For the human eye it would be almost impossible to spot the anomaly.

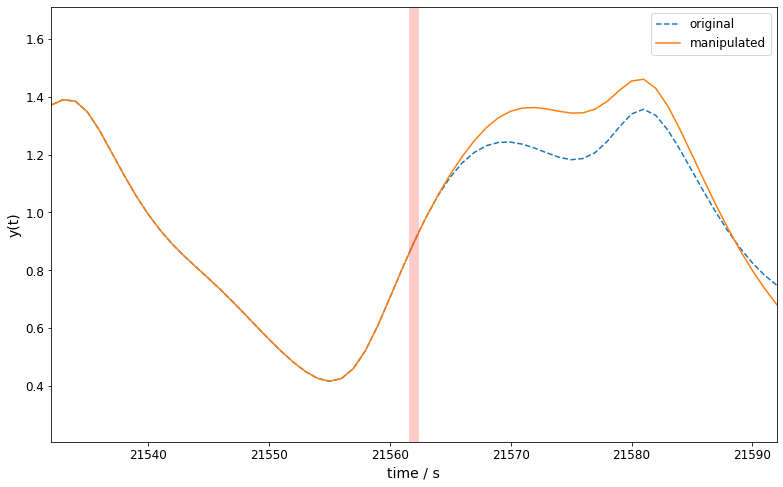Example Anomaly in a MG time series 1 Example Anomaly in a MG time series 1<br> Figure 2: Top: Example for the creation of a Mackey-Glass time series with a temporal anomaly. The original time series (dashed line) is manipulated in such a way, that a segment is removed and the two remaining ends are joined together. In this example, the interval [21562,21703] is removed from the original curve. The resulting manipulated time series (solid line) has a smooth point of connection, but significantly differs from the original. Bottom: Zoomed-In. The red shaded area indicates the position where the anomaly was inserted.

Adding Noise

For the 10 time series of this benchmark, in total 100 anomalies were inserted (10 anomalies per time series). In the last step, in order to increase the complexity of the anomaly detection task slightly, we add noise drawn from a random uniform distribution with the range [-0.01, 0.01] to each point of all time series.

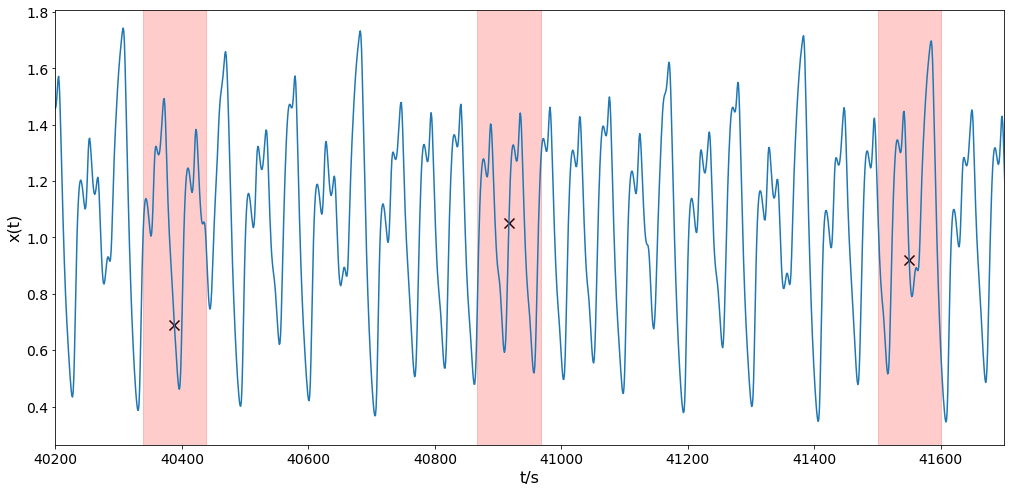Anomalous Mackey-Glass Time Series with revealed Anomalies Figure 3: This graph shows the same section of a Mackey-Glass time series as the first graph on this page, but now reveals the location of the anomalies in the time series. The anomalies are at t<sub>1</sub> = 40388, t<sub>2</sub>=40917 and t<sub>3</sub>=41550. The positions are indicated by the black crosses in the plot.

Generating your own MGAB Benchmark

Based on the procedure described in the previous section, it is also possible to adjust different parameters and generate an own MGAB with steerable size and difficulty.

Dependencies

The following dependencies are required for running the code on all operating systems. In the parentheses we add the version, which we used for our experiments.

Usage

The main function of this module is generate_benchmark(args). All parameters are passed to this function through a Python dictionary. It is possible to pass an empty dictionary or no argument at all. Typically, one would specify a subset of the required parameters in the dictionary; the function would then use the default values for the remaining parameters.

Usage:

import mgab
benchmark_list = mgab.generate_benchmark(args)

generate_benchmark(args:dict={'reproduce_original_mgab':'use_precomputed_mg'})

Generates a MGAB according to the specifications of the user. A list of MG time series with a certain number of anomalies is created. The created time series can be directly written to CSV-files and/or returned by this function and processed further.

Examples

# Generate the original MGAB. This will create a directory "mgab" (if not existant yet),
# and write the 10 CSV-files containing the 10 time series into this folder. These CSV-
# files should be exactly the same as the original ones in this repository.
import mgab
original_mgab = mgab.generate_benchmark()

# Generate some customized new benchmark. We can change a few of the default parameters.
import mgab
my_new_benchmark = mgab.generate_benchmark({ # we choose a few parameters ourselves
        'output_dir' : 'my_new_benchmark', # specify new directory for the output files
        'output_force_override': True, # Override files, if necessary
        'num_series': 3, # Create only 3 time series for this benchmark
        'series_length': 10000, # Only create time series of lenth 10k
        'num_anomalies' : 5, # Each time series contains 5 anomalies
        'noise' : 'rnd_uniform',# Add random uniform noise
        'noise_param' : (-0.01, 0.01), # range for random uniform noise
        'min_anomaly_distance' : 200, # Anomalies have to have a distance of at least 200
        'mg_tau' : 30, # use a larger value for tau
        'mg_ts_path_load' : None, # We do not have any pre-computed MG time series. So generate it with the DDE solver
        'mg_ts_dir_save' : "./data/" # Save the generated MG time series of the DDE solver in the data directory. This 
                                     # allows us, to reuse it again (e.g., if we want to change the number of anomalies)
     })